Descobreix com funciona una contrarellotge entrant al Concurs de prova:
Visita les pàgines dels concursos finalitzats per veure els enunciats i solucions.
Registra't en 1 minut i t'informarem de les properes convocatòries:
Queden 2 setmanes i 4 dies per respondre.
| Nivell | Medalles |
|---|---|
| 2n d'ESO | 1122 |
| 4t d'ESO | 8266 |
| 2n de Batxillerat | 31 |
Contrarellotge temàtica: animals
Nivell: 2n de Batxillerat
Diumenge, 10 de febrer de 2019 a les 19:00
×
23 participants
×
135 participants virtuals
Contrarellotge temàtica: animals
Nivell: 4t d'ESO
Diumenge, 3 de febrer de 2019 a les 19:00
×
51 participants
×
114 participants virtuals
Contrarellotge temàtica: animals
Nivell: 2n d'ESO
Diumenge, 27 de gener de 2019 a les 19:00
×
71 participants
×
356 participants virtuals
Descobreix com funciona una contrarellotge entrant al Concurs de prova:
Visita les pàgines dels concursos finalitzats per veure els enunciats i solucions.
Registra't en 1 minut i t'informarem de les properes convocatòries:
Després d'un merescut descans durant l'estiu, avui 1 de setembre encetem el nou curs a la Contrarellotge Matemàtica publicant els tres primers Problemes del mes. Com vam fer l'any passat, des de setembre i fins a juny, cada mes us plantejarem 3 problemes que podreu respondre durant tot el mes.
Aquest curs hem previst realitzar dues sèries de tres contrarellotges, que tindran lloc a finals d'octubre i a principis de març. També tenim pensades altres novetats que anirem anunciant durant el curs.
Molta sort a tothom!
L'estudiant Izan Beltrán ens ha enviat una solució alternativa al problema 15 de la Contrarellotge de 2n d'ESO del passat diumenge, molt més senzilla que la solució oficial. Aquí us reproduïm el problema perquè el penseu una mica, i també la solució d'Izan.
Tenim peces de domino de iguals.
De quantes maneres diferents podem cobrir un tauler de ?
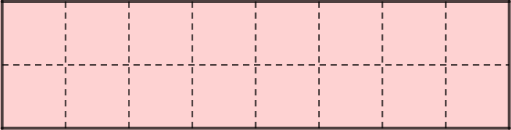
Per exemple, aquesta és una configuració vàlida:
Anomenem $F_{n}$ el nombre de formes que tenim d'omplir un rectangle de mida $2\times n$ com el següent:
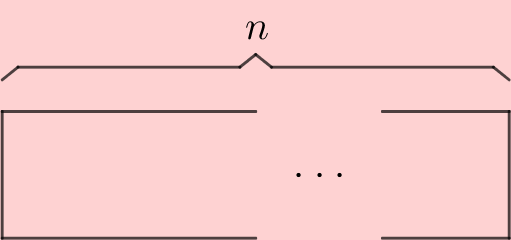
Començant a omplir per l'esquerra, tenim dues opcions: o bé posem una peça vertical, o bé posem dues peces horitzontals:
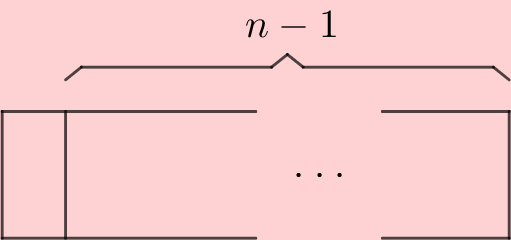
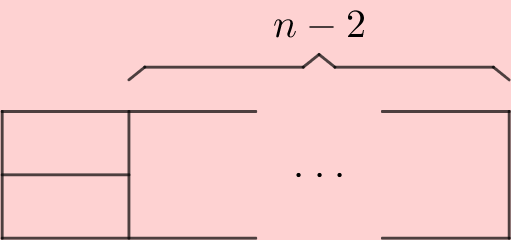
En el primer cas, podrem omplir el rectangle que queda de $F_{n-1}$ formes, i en el segon, de $F_{n-2}$ formes.
Per tant, hem trobat la següent recurrència: $$ F_n=F_{n-1}+F_{n-2} $$
Es tracta de la successió de Fibonacci! Calculem ara els termes inicials.
Quan tenim un tauler de $2\times1$, només podem posar una peça vertical: $$F_1=1$$
Quan tenim un de $2\times2$, podem posar-ne dues verticals o dues horitzontals: $$F_2=2$$
I per la fórmula de la recurrència, trobem la successió: $$\{F_n\}=1,2,3,5,8,13,21,34,\ldots$$ I la solució és: $$F_8=34$$
Les properes contrarellotges (i últimes del curs 2017/18), queden convocades pels diumenges 3 de juny (2n d'ESO) i 10 de juny (4t d'ESO). Excepcionalment, i degut a la proximitat de les Proves d'Accés a la Universitat, no realitzarem la prova de 2n de batxillerat. Els problemes tindran la temàtica comuna dels jocs i esports.
Per que us entretingueu fins les proves, us animem a jugar algunes partides al joc del Nim —joc que té unes propietats matemàtiques molt interessants. Per si no el coneixeu, a continuació us expliquem les normes.
Fem unes piles de pedres (o llumins, cartes, o senzillament segments dibuixats en un paper), cada pila amb la quantitat que vulguem d'ítems. Per exemple:
En torns alternatius, cada jugador retira tantes pedres com vulga d'una de les piles; i sempre ha de treure, com a mínim, una pedra. Perdrà el jugador que es quede amb l'última pedra.
Avui presentem una petita novetat: els noms dels usuaris ara van precedits per un símbol que indica el seu curs o estatus. A continuació teniu la llista completa de símbols:
| Llista de símbols de nivell |
|---|
| Primària |
| 1r d'ESO |
| 2n d'ESO |
| 3r d'ESO |
| 4t d'ESO |
| 1r de Batxillerat, cicle grau mitjà |
| 2n de Batxillerat |
| Universitat, cicle de grau superior |
| Professor/a |
| Altres, curs no especificat |
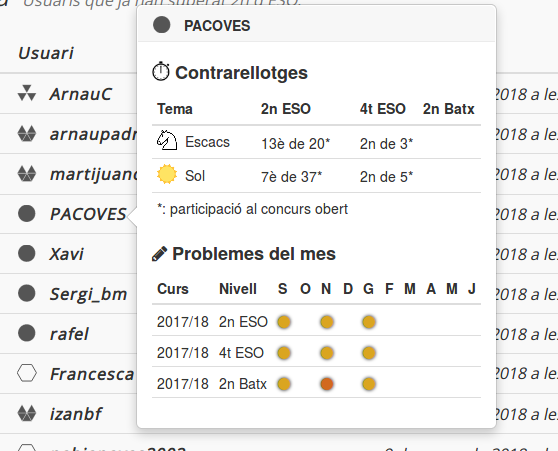
Actualització 1/2/2018: a més, ara també podeu clicar els noms d'usuari i veureu una caixa amb un resum de les participacions d'aquest usuari a les diverses proves de la Contrarellotge matemàtica, com mostra la següent imatge:
Avui convoquem la propera sèrie de Contrarellotges, i amb l'objectiu que us serveixin d'entrenament per les Proves Cangur, els problemes seran una tria dels problemes d'edicions passades del Cangur.
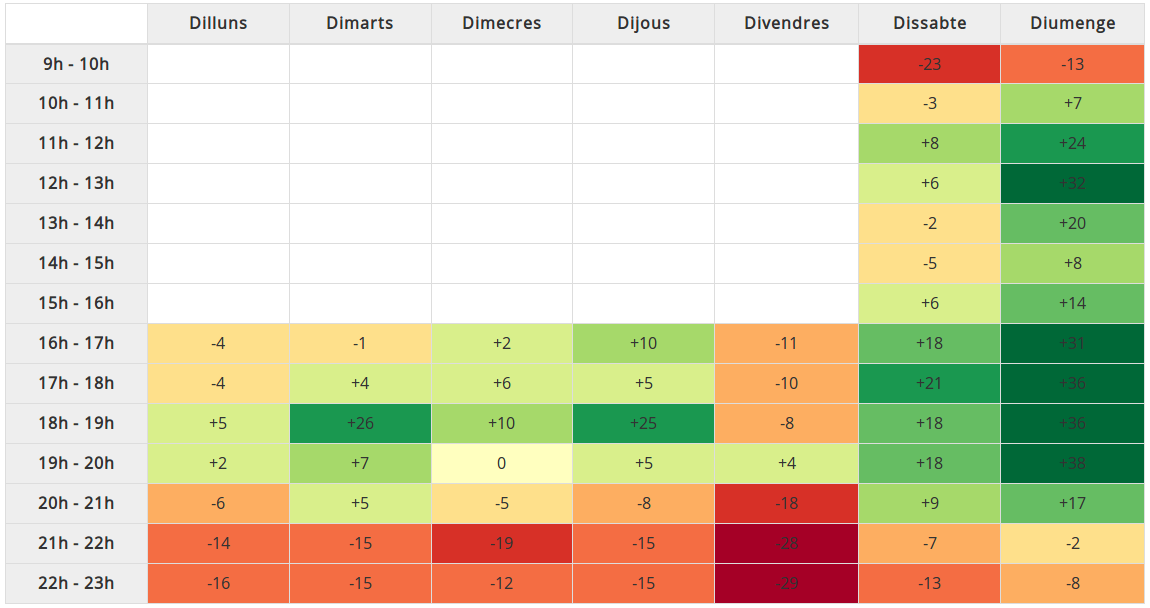
A la vista dels resultats de l'enquesta horària, hem decidit realitzar aquestes Contrarellotges els diumenges 18 de febrer, 25 de febrer i 4 de març de 19 h a 20 h.
Esperem que gaudiu amb els problemes!
En aquest article al meu blog he explicat com està implementada la Contrarellotge matemàtica: els llenguatges de programació emprats, l'arquitectura del sistema, i totes les eines que fan funcionar aquesta plataforma.
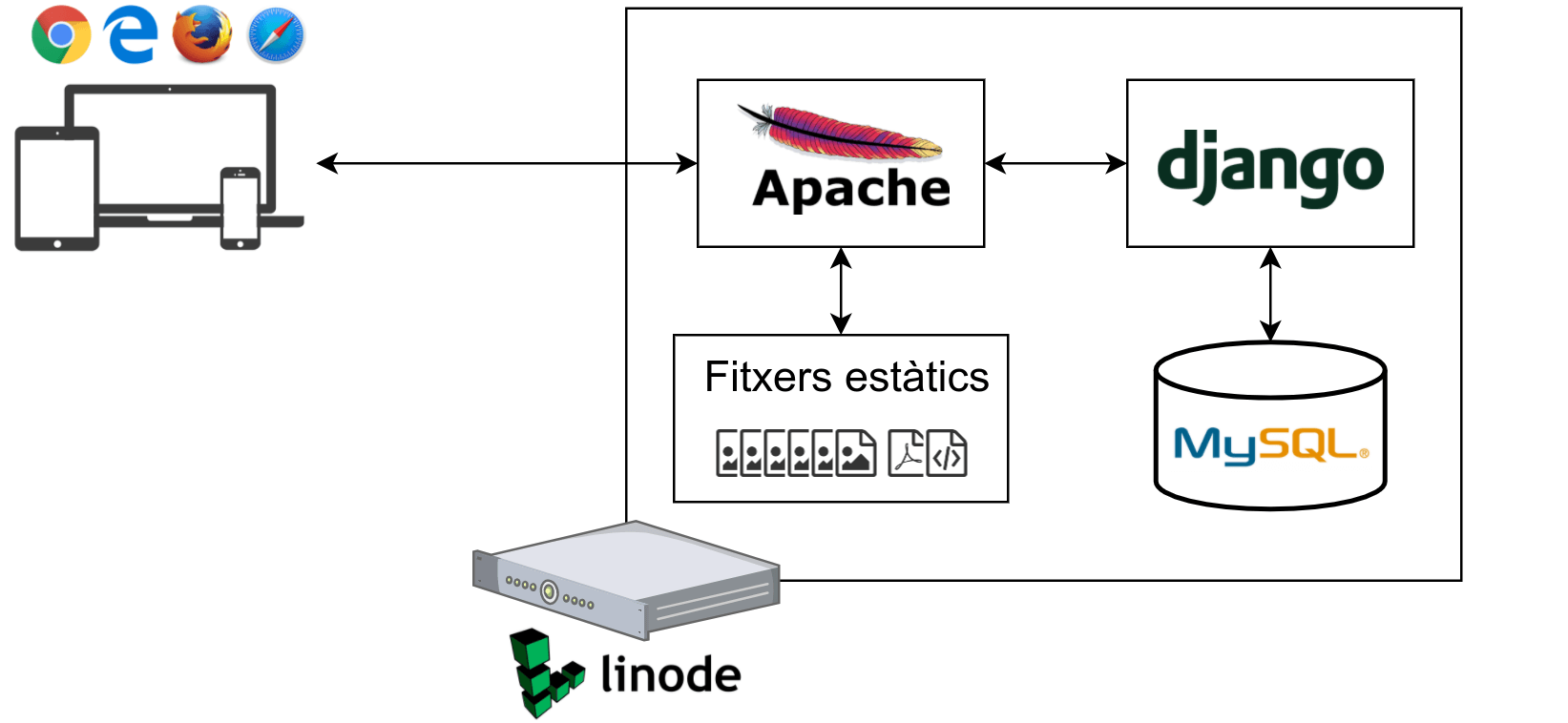Aquest és un dels esquemes sobre l'arquitectura del sistema que explico a l'article.