Contrarellotge temàtica: els escacs (2n de Batxillerat)
Dilluns, 5 de juny de 2017 a les 19:00

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

La contrarellotge s'ha acabat amb èxit!

Enhorabona al guanyador de la prova oficial: jolivetti!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Llancem $6$ daus. Quants valors diferents pot prendre la suma dels nombres que hem obtingut?
A. $29$
B. $30$
C. $31$
D. $32$
E. $33$
En blanc
Mostra solució

Com a mínim obtindrem un $1$ a cada dau, i la suma serà $6\cdot1=6$; com a màxim, obrindrem un $6$ a cada dau, i la suma serà $6\cdot6=36$.

En total, podem obtindre $36-6+1=31$ resultats diferents (hem de sumar $1$ perquè ambdós resultats estan inclosos).

Problema 2
3 punts   •   1 min 30 s

Tenim les $32$ peces d'un joc d'escacs guardades en una caixa. Si treiem les peces a l'atzar, quantes peces hem de traure com a mínim per assegurar-nos que hem tret $2$ peons negres?
A. $16$
B. $24$
C. $26$
D. $28$
E. $32$
En blanc
Mostra solució
En el pitjor dels casos, traurem totes les peces blanques $(16)$, totes les peces majors negres $(8)$ i finalment els $2$ peons negres. En total, haurem tret: $$\text{n. peces} = 16+8+2 = 26$$

Problema 3
3 punts   •   1 min 30 s

Hem dividit un hexàgon regular de costat $3$ en triangles equilàters de costat $1$, tal com es veu a la figura:

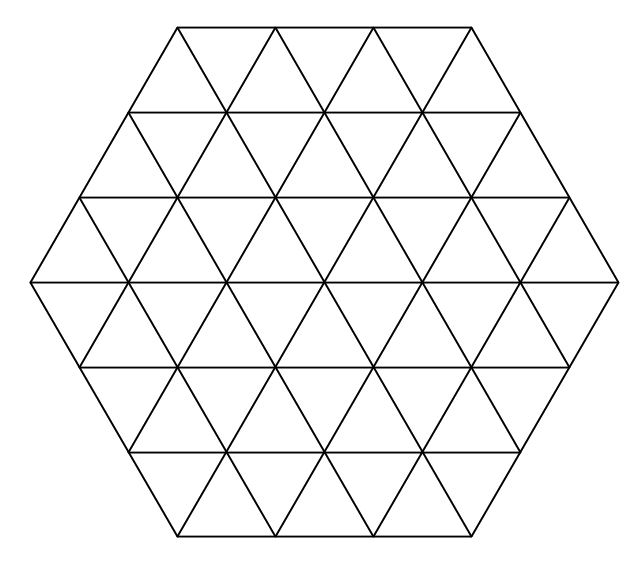
Quants segments de longitud $1$ diferents hi ha a la figura?

A. $60$
B. $90$
C. $54$
D. $72$
E. $64$
En blanc
Mostra solució
Primer, sumarem els segments horitzontals. Si comencem per dalt, tenim $7$ files amb els següents segments: $$n_{\text{horitzontals}}=3+4+5+6+5+4+3=30$$ Tindrem el mateix nombre de segments en les dues direccions "inclinades". En total: $$n_{\text{total}}=3\cdot30=90$$

Problema 4
3 punts   •   1 min 30 s

Cada matí, Josep es menja el $20\%$ dels caramels que hi ha a un pot. El segon dia a la tarda, queden $32$ caramels al pot.

Quants caramels hi havia al pot inicialment?

A. $40$
B. $50$
C. $55$
D. $60$
E. $75$
En blanc
Mostra solució
Anomenem $x$ el nombre inicial de caramels. Cada matí, Josep deixa el $80\%$ dels caramels al pot, és a dir, multiplica per $0.8$ el nombre de caramels que queden. Després de dos dies, quedaran: $$x\cdot0.8\cdot0.8=32$$ Resolem l'equació: $$0.64\cdot x=32\quad\Rightarrow\quad x=\frac{32}{0.64}=50$$

Problema 5
3 punts   •   1 min 30 s

Les equacions $2x+7=3$, i $bx-10=-2$ tenen la mateixa solució per $x$. Quant val $b$?
A. $-8$
B. $-4$
C. $-2$
D. $4$
E. $8$
En blanc
Mostra solució
De la primera equació deduim que: $$2x+7=3\quad\Rightarrow\quad 2x=-4\quad\Rightarrow$$ $$\Rightarrow\quad x=-2$$ I substituint a la segona tenim: $$b\cdot(-2)-10=-2\quad\Rightarrow\quad -2b=8\quad\Rightarrow$$ $$\Rightarrow\quad b=-4$$

Problema 6
4 punts   •   3 min

Quantes fitxes de dominó $(2\times1)$ necessitem per cobrir un tauler d'escacs al qual li hem retallat les caselles de dues cantonades, com a la següent figura? (Cada meitat de la peça de dominó ha de coincidir amb una casella del tauler).

A. $64$
B. $63$
C. $32$
D. $31$
E. No es pot
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Els costats d'un triangle mesuren $6$, $8$ i $10$. Quina és la longitud de l'altura més curta d'aquest triangle?
A. $5$
B. $4.5$
C. $3$
D. $6$
E. $4.8$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

Quin és el màxim nombre de cavalls que podem situar a un tauler d'escacs sense que cap d'ells n'amenaci cap altre?

A. $8$
B. $12$
C. $16$
D. $24$
E. $32$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Un arc de $60^\circ$ del cercle $A$ té la mateixa longitud que un arc de $90^\circ$ del cercle $B$. Si l'àrea del cercle $A$ és $1$, quant mesura l'àrea del cercle $B$?
A. $\frac49$
B. $\frac23$
C. $\frac56$
D. $\frac32$
E. $\frac94$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

Tenim $8$ quadradets de fusta, $4$ blancs i $4$ negres. Si els posem en fila, en ordre aleatori, quina és la probabilitat que ens quede una fila del tauler d'escacs? És a dir, d'una de les dues formes:

A. $\frac1{20}$
B. $\frac1{35}$
C. $\frac1{42}$
D. $\frac1{32}$
E. $\frac1{45}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

Situem un cavall al centre del tauler:

Per cada casella del tauler, comptem quin és el mínim nombre de salts de cavall que ens calen per arribar-hi. Per exemple, hi ha algunes caselles $(8)$ que estan a $1$ salt de cavall. D'altres, estan a $2$ salts de cavall, etc.

Anomenem caselles llunyanes aquelles que estan a més salts de cavall que cap altra. Quantes caselles llunyanes hi ha al tauler?

A. $3$
B. $4$
C. $5$
D. $6$
E. $8$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Quatre cercles de radi $1$ són tangents exteriors a un cercle de radi $2$ i tangents interiors a un quadrat, tal com es mostra a la figura:

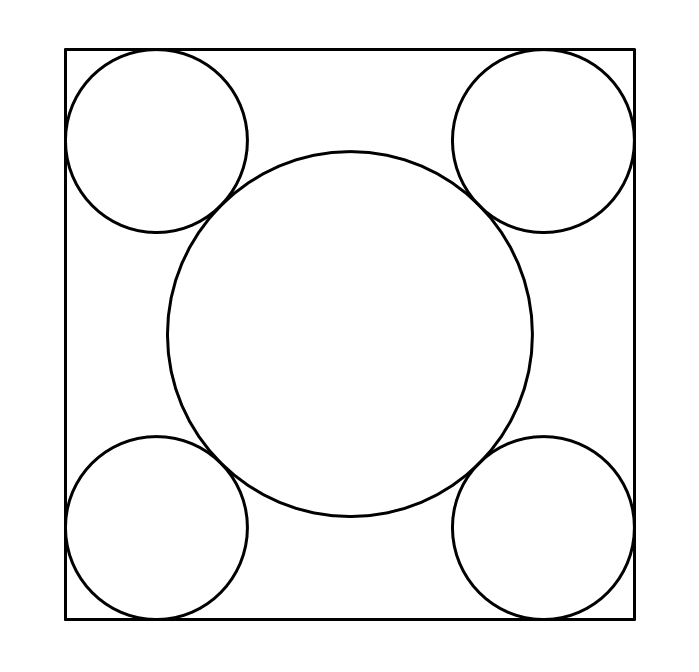
Quina és l'àrea del quadrat?

A. $32$
B. $22+12\sqrt2$
C. $16+12\sqrt3$
D. $48$
E. $36+16\sqrt2$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

Anomenem rei coix un rei d'escacs que només es pot moure cap a dalt o cap a la dreta:

Un rei coix va des de la casella de sota a l'esquerra fins a la casella de dalt a la dreta. Si a cada passa es mou amb igual probabilitat cap a la dreta o cap a dalt, quina és la probabilitat que en el seu camí passe per la casella marcada amb un cercle vermell?

A. $\frac{1}{572}$
B. $\frac{21}{143}$
C. $\frac{21}{286}$
D. $\frac{42}{143}$
E. $\frac{63}{143}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

Sigui $a_1,a_2,\ldots$ una successió amb les següents propietats:

  • $a_1=1$
  • $a_{2n}=n\cdot a_n$, per qualsevol enter $n$.
Quant val $a_{2^{100}}$?
A. $1$
B. $2^{99}$
C. $2^{100}$
D. $2^{4950}$
E. $2^{9999}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

Considerem tres cercles concèntrics de radis $1,2,3$, tallats per dues rectes que passen pel centre. Quant mesura l'angle $\alpha$ de la figura (en radians) si sabem que la zona grisa representa $\frac{8}{13}$ de l'àrea blanca?
A. $\frac\pi4$
B. $\frac\pi5$
C. $\frac\pi6$
D. $\frac\pi7$
E. $\frac\pi8$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat o un curs inferior.

# Usuari Punts Respostes
1. 1b  jolivetti 84,75 ◌
2. 4e  arnaupa... 59,75 ◌ ◌ ◌
3. 1b  AndreuV... 56,0
4. 4e  martiju... 41,75 ◌ ◌ ◌ ◌ ◌ ◌
5. 1b  isaaclemon 29,25 ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌
6. 4e  selaco 21,75 ◌ ◌ ◌ ◌

Concurs obert
Usuaris que han superat 2n de Batxillerat, professors, etc.

# Usuari Punts Respostes
1. Professor/a  jacques 52,75 ◌ ◌ ◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. 4e  CesarMG 92,75
2. Universitat  Melany2276 80,0
3. Curs indeterminat  Origami... 66,5 ◌
4. Universitat  Clàudiaa 63,0
5. Universitat  MarcJB 48,0 ◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta