Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
Enhorabona a tots els participants!
I especialment als guanyadors de la prova oficial: jolivetti, pcartanya i Euclidianna.
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
$5$ pintors triguen $5$ dies a pintar $5$ habitacions.
Quants dies triguen $10$ pintors a pintar $10$ habitacions?
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Avui estem a $10/3/2017$. Aquesta data conté els dígits $0$ i $1$ dos cops cadascun.
Quants dies falten per al proper dia en què la data contindrà un mateix dígit repetit com a mínim $4$ cops? (Si fóra demà, faltaria $1$ dia).
Si volem el dígit repetit $4$ cops l'any $2017$, aquest dígit només podrà ser l'$1$ o el $2$.
En el cas del $2$, només hi ha una data que ho compleix: $22/12/2017$.
Per repetir $4$ cops l'$1$, necessitem tres uns en el dia i el mes. Hi ha diverses formes:
- $11/10$
- $1/11,\; 10/11,\; 11/11,\; 12/11,\;\ldots,\; 21/11$
- $11/12$
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Sabem que hi ha un sol amagat en un dels tres cofres:

Cada cofre té una nota amb una frase escrita, i sabem que només una d'elles diu la veritat. Diuen:
- El sol no està aquí.
- El sol no està aquí.
- El sol està al cofre $2$.
A quin cofre està el sol?
Esbrinem primer quina frase és la correcta.
Si la $1$ és correcta, llavors les altres dues són falses. Però si la $2$ és falsa, el sol està al cofre $2$ i llavors la frase $3$ hauria de ser certa. No pot ser.
Si la $2$ és correcta, llavors la $1$ és falsa i el sol està al cofre $1$. La $3$ també ha de ser falsa, i efectivament ho és. Per tant, el sol ha d'estar al cofre $1$.
Finalment, vegem que la $3$ no pot ser certa, perquè llavors la $1$ seria certa també.
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
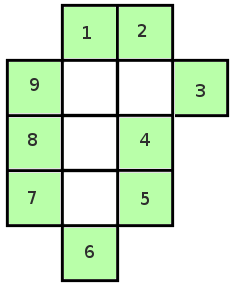
Partint d'aquesta peça del Tetris:

Quantes figures diferents podem obtenir afegint-li un quadrat? El quadrat nou ha de tenir un costat coincident amb un dels quadrats de la figura.
Podem afegir el quadrat a qualsevol de les $9$ posicions possibles i totes les figures resultants seran diferents:
Problema 6
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
Com alguns ja sabreu, el Sol és una estrella activa que sovint produeix erupcions solars $(E)$ i explosions de gas $(G)$, les quals els astrònoms sempre vigilen perquè poden danyar els satèl·lits i els astronautes.
Certa setmana hi han hagut dues erupcions $(E)$ en dies diferents. D'altra banda, i de manera independent, hi han hagut dues explosions de gas $(G)$ en dies consecutius.
Quina és la probabilitat que no hagen coincidit cap explosió i erupció en el mateix dia?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Siguin dos semicercles, inscrit un dintre de l'altre, amb les bases coincidents i tangents per l'esquerra. Dibuixem una corda
paral·lela a les bases dels semicercles, i tangent al semicercle petit,
i observem que mesura $4$. Tal com es veu a la figura:
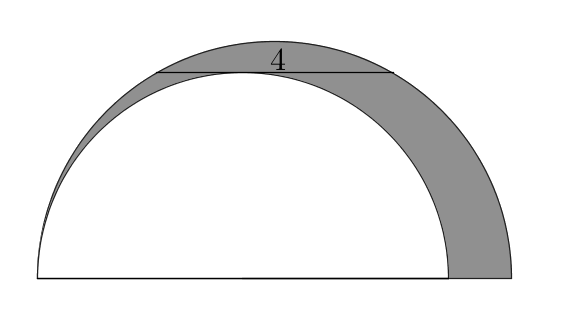 Quant mesura l'àrea ombrejada?
Quant mesura l'àrea ombrejada?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Considerem els punts mitjos de tres arestes d'un cub, tal com veiem a la figura:
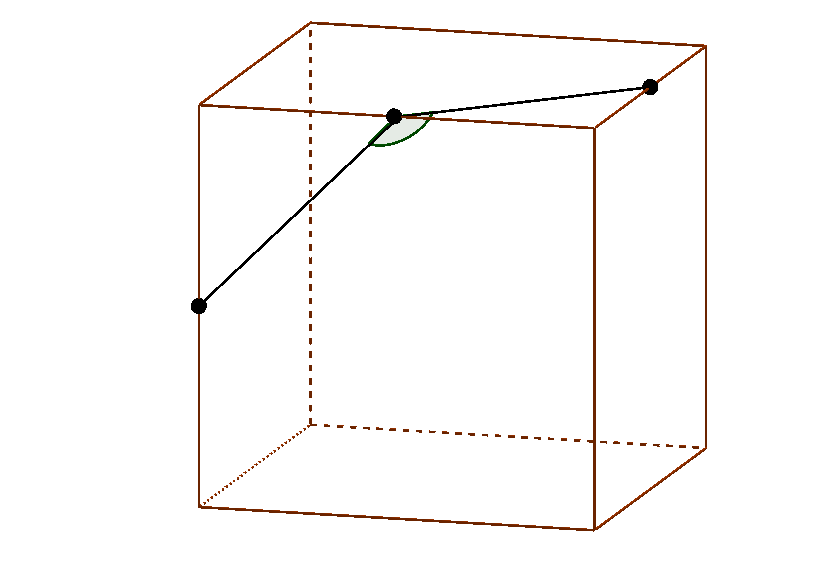
Quant mesura l'angle que formen?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Considerem el quadrat $ABCD$ de costat unitat, on anomenem $M$ el punt mig del costat $BC$ i $N$ el punt mig del segment $BM$. Unim $M$ i $N$ amb el vèrtex $A$, i dibuixem la diagonal $BD$:
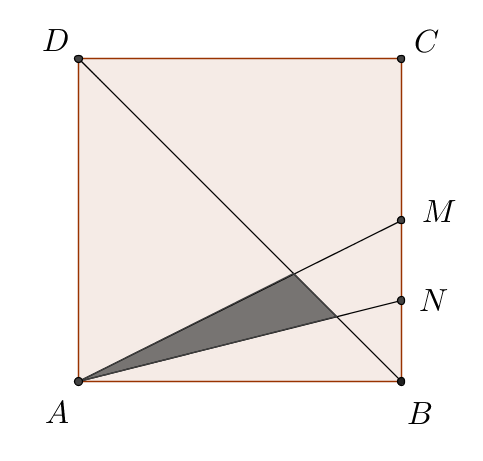 Quant mesura l'àrea ombrejada?
Quant mesura l'àrea ombrejada?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat o un curs inferior.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | jolivetti | jolivetti | 72,75 | ◌ ◌ ◌ | ||||||||||||
| 2. | pcartanya | pcartanya | 70,25 | ◌ | ||||||||||||
| 3. | Euclidi... | Euclidianna | 52,75 | |||||||||||||
| 4. | VictorE... | VictorEscudero | 37,0 | ◌ ◌ ◌ ◌ | ||||||||||||
| 5. | Gauss | Gauss | 36,0 | ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 6. | Euler | Euler | 33,75 | ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 7. | doncipo... | doncipotedelamancha | 29,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 8. | Innigo | Innigo | 28,25 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 9. | Alpha | Alpha | 27,25 | |||||||||||||
| 10. | Deixebl... | DeixebledeJosepMaria | 26,5 | ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 11. | Lluis | Lluis | 26,0 | ◌ ◌ | ||||||||||||
| 12. | Anaxima... | Anaximandre | 21,25 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 13. | Chemapr... | Chemaprovamcrack | 17,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 14. | laiaruiz | laiaruiz | 16,0 | ◌ ◌ ◌ ◌ ◌ ◌ |
Concurs obert
Usuaris que han superat 2n de Batxillerat, professors, etc.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|
| 1. | Eugeni.C.S | Eugeni.C.S | 99,0 | ||||||
| 2. | polrt | polrt | 15,25 | ◌ ◌ ◌ ◌ ◌ |
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta



 D'entre els quatre asos de la baralla anglesa (dos negres i dos vermells), triem dues cartes a
l'atzar. Quina és la probabilitat que triem dues cartes del mateix color?
D'entre els quatre asos de la baralla anglesa (dos negres i dos vermells), triem dues cartes a
l'atzar. Quina és la probabilitat que triem dues cartes del mateix color?
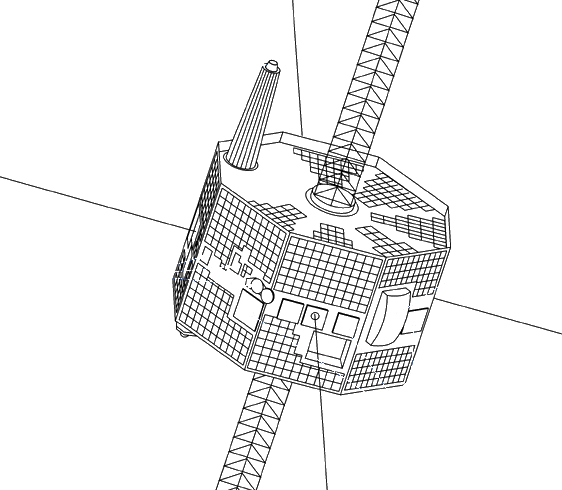 Considerem un satèl·lit amb forma de prisma rectangular amb les bases formades
per octàgons regulars. Si té una altura de $2\text{ m}$ i el costat
dels octàgons és d'$1\text{ m}$, quant mesura l'àrea de la superfície
del prisma?
Considerem un satèl·lit amb forma de prisma rectangular amb les bases formades
per octàgons regulars. Si té una altura de $2\text{ m}$ i el costat
dels octàgons és d'$1\text{ m}$, quant mesura l'àrea de la superfície
del prisma?