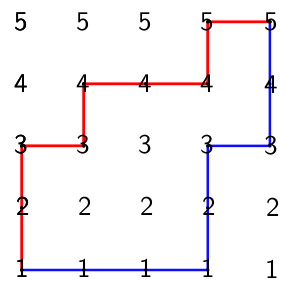
Un cargol es mou seguint les línies d'una quadrícula $5$x$5$ com a la figura. Comença abaix a l'esquerra i es mou només cap a la dreta ($\rightarrow$) o cap amunt ($\uparrow$), fins arribar a dalt a la dreta.
Com que va tan lent, s'avorreix i decideix fer un joc: va multiplicant tots els números per sobre dels quals passa.
Quants camins pot seguir el cargol de manera que el resultat del producte sigui un quadrat perfecte?
Per exemple, al camí vermell acaba amb el producte $1\cdot 2\cdot 3^2\cdot 4^3 \cdot 5^2 = 28800$; mentre que el blau, amb $1^4\cdot 2 \cdot 3^2 \cdot 4 \cdot 5 = 360$, cap dels dos un quadrat.
Un número és un quadrat perfecte si tots els seus factors primers tenen un exponent parell.
Per exemple, $4 = 2^2$ o $571536 = 2^4 \cdot 3^6 \cdot 7^2 $ són quadrats perfectes, però $45 = 3^2 \cdot 5^1$ no.
Com que $2, 3$ i $5$ no són quadrats perfectes, haurem de passar un nombre parell de vegades per cada un d'ells.
L'últim pas ha de ser horitzontal.
La solució és un nombre menor que $5$.
Cal notar que per tal que el producte sigui un quadrat, haurem de passar per un nombre parell de vegades per $5$'s, $3$'s i $2$'s. D'altra banda, podem passar per tants $4$'s i $1$'s com vulguem.
Ara, per construir els camins començarem des del final.
En primer lloc, cal notar que l'últim pas ha de ser horitzontal ja que, si no, només tindríem un $5$ al producte final.

Ara, podem provar que passa si continuem per la fila dels $5$'s. En aquest cas, haurem de passar per sobre de quatre $5$'s, però llavors quan baixem no tindrem espai per afegir un nombre parell de $3$'s i de $2$'s.
Per tant, ens veiem obligats a baixar a la fila dels $4$'s. Ens queden per fer tres moviments horitzontals, i hem de passar mínim per dos $2$'s i dos $3$'s.
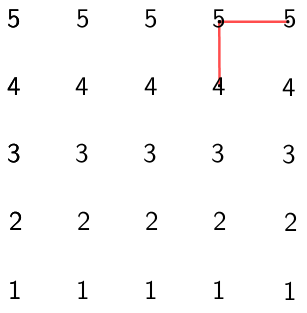
Si passem quatre cops per un d'aquests, no tindrem espai a afegir el mínim de l'altre. És a dir, el nostre camí haurà de tenir exactament dos $2$'s i dos $3$'s.
I ara ja és evident que els únics camins que ens van bé són els següents
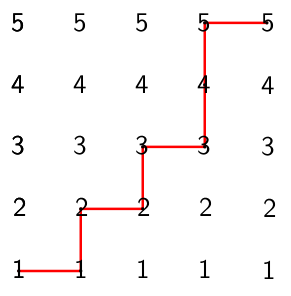
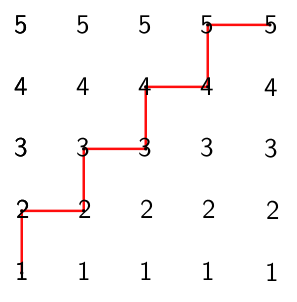
Que ens donen un resultat de $1^2 \cdot 2^2 \cdot 3^2 \cdot 4 \cdot 5^2 = 60^2$ i $1 \cdot 2^2 \cdot 3^2 \cdot 4^2 \cdot 5^2 = 120^2 $, respectivament.
És a dir, el cargol pot seguir $\boxed{2}$ camins diferents.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | jaquerol | jaquerol | 1 de març de 2020 a les 8:44 | 01/03/2020 |
| Or | jofre | jofre | 1 de març de 2020 a les 8:45 | 01/03/2020 |
| Or | Jogaal | Jogaal | 1 de març de 2020 a les 9:53 | 01/03/2020 |
| Or | beatriz_al... | beatriz_alarcon | 2 de març de 2020 a les 10:51 | 02/03/2020 |
| Or | mclotet | mclotet | 6 de març de 2020 a les 20:27 | 06/03/2020 |
| Or | Alexandra.A | Alexandra.A | 17 de març de 2020 a les 11:48 | 17/03/2020 |
| Or | Marta09 | Marta09 | 24 de març de 2020 a les 16:29 | 24/03/2020 |
| Or | nadia.R.L | nadia.R.L | 31 de març de 2020 a les 10:22 | 31/03/2020 |
| Or | martinos | martinos | 31 de març de 2020 a les 10:50 | 31/03/2020 |
| Plata | IGG | IGG | 20 de març de 2020 a les 17:38 | 20/03/2020 |
| Plata | joan.s.e | joan.s.e | 31 de març de 2020 a les 13:23 | 31/03/2020 |
| Bronze | Eugeni.C.S | Eugeni.C.S | 16 de març de 2020 a les 11:00 | 16/03/2020 |
| Bronze | DiegoT | DiegoT | 24 de març de 2020 a les 15:30 | 24/03/2020 |
| Xocolata | JOFRE.ciberta | JOFRE.ciberta | 1 de març de 2020 a les 8:44 | 01/03/2020 |
| Xocolata | dianaaaa88 | dianaaaa88 | 3 de març de 2020 a les 14:41 | 03/03/2020 |
| Xocolata | Guillem.C.M | Guillem.C.M | 15 de març de 2020 a les 10:47 | 15/03/2020 |
| Xocolata | Bruno.Costan | Bruno.Costan | 30 de març de 2020 a les 15:57 | 30/03/2020 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | jorhermar45 | jorhermar45 | 1 de març de 2020 a les 1:55 | 01/03/2020 |
| Or | luca.passo... | luca.passolini2017 | 1 de març de 2020 a les 8:43 | 01/03/2020 |
| Or | PauCantos | PauCantos | 1 de març de 2020 a les 10:49 | 01/03/2020 |
| Or | Nomarolbap | Nomarolbap | 1 de març de 2020 a les 11:18 | 01/03/2020 |
| Or | rsempere | rsempere | 1 de març de 2020 a les 12:12 | 01/03/2020 |
| Or | arakelov | arakelov | 1 de març de 2020 a les 12:27 | 01/03/2020 |
| Or | Eva | Eva | 2 de març de 2020 a les 13:33 | 02/03/2020 |
| Or | mikiblsinc... | mikiblsince2005 | 3 de març de 2020 a les 9:46 | 03/03/2020 |
| Or | PepBorras | PepBorras | 4 de març de 2020 a les 14:24 | 04/03/2020 |
| Or | enriquervwtf | enriquervwtf | 6 de març de 2020 a les 10:04 | 06/03/2020 |
| Or | rmates | rmates | 6 de març de 2020 a les 20:11 | 06/03/2020 |
| Or | evmogi | evmogi | 14 de març de 2020 a les 12:24 | 14/03/2020 |
| Or | Euler | Euler | 16 de març de 2020 a les 20:43 | 16/03/2020 |
| Or | Marta1876 | Marta1876 | 21 de març de 2020 a les 19:48 | 21/03/2020 |
| Or | macamaca | macamaca | 24 de març de 2020 a les 15:29 | 24/03/2020 |
| Or | JoanAn | JoanAn | 30 de març de 2020 a les 13:06 | 30/03/2020 |
| Plata | montserrat... | montserrat.muria | 1 de març de 2020 a les 16:47 | 01/03/2020 |
| Plata | Sergi_bm | Sergi_bm | 1 de març de 2020 a les 19:50 | 01/03/2020 |
| Plata | Trapellí | Trapellí | 1 de març de 2020 a les 20:21 | 01/03/2020 |
| Plata | PauMB | PauMB | 1 de març de 2020 a les 20:30 | 01/03/2020 |
| Plata | nou | nou | 4 de març de 2020 a les 23:49 | 04/03/2020 |
| Plata | AAM_mathsb... | AAM_mathsbooks | 12 de març de 2020 a les 8:23 | 12/03/2020 |
| Plata | Francesc16... | Francesc162005 | 13 de març de 2020 a les 14:10 | 13/03/2020 |
| Plata | PACOVES | PACOVES | 16 de març de 2020 a les 12:51 | 16/03/2020 |
| Plata | nuriaishons | nuriaishons | 24 de març de 2020 a les 16:28 | 24/03/2020 |
| Plata | Farrius | Farrius | 26 de març de 2020 a les 13:47 | 26/03/2020 |
| Plata | Guille | Guille | 30 de març de 2020 a les 16:35 | 30/03/2020 |
| Xocolata | enavas08 | enavas08 | 20 de març de 2020 a les 12:20 | 20/03/2020 |
| Xocolata | EricN | EricN | 30 de març de 2020 a les 11:43 | 30/03/2020 |
| Xocolata | ErikF | ErikF | 30 de març de 2020 a les 13:08 | 30/03/2020 |
