El rectangle de la figura està partit en $9$ quadrats diferents. L'alçada del rectangle és $32$. Quina amplada té?
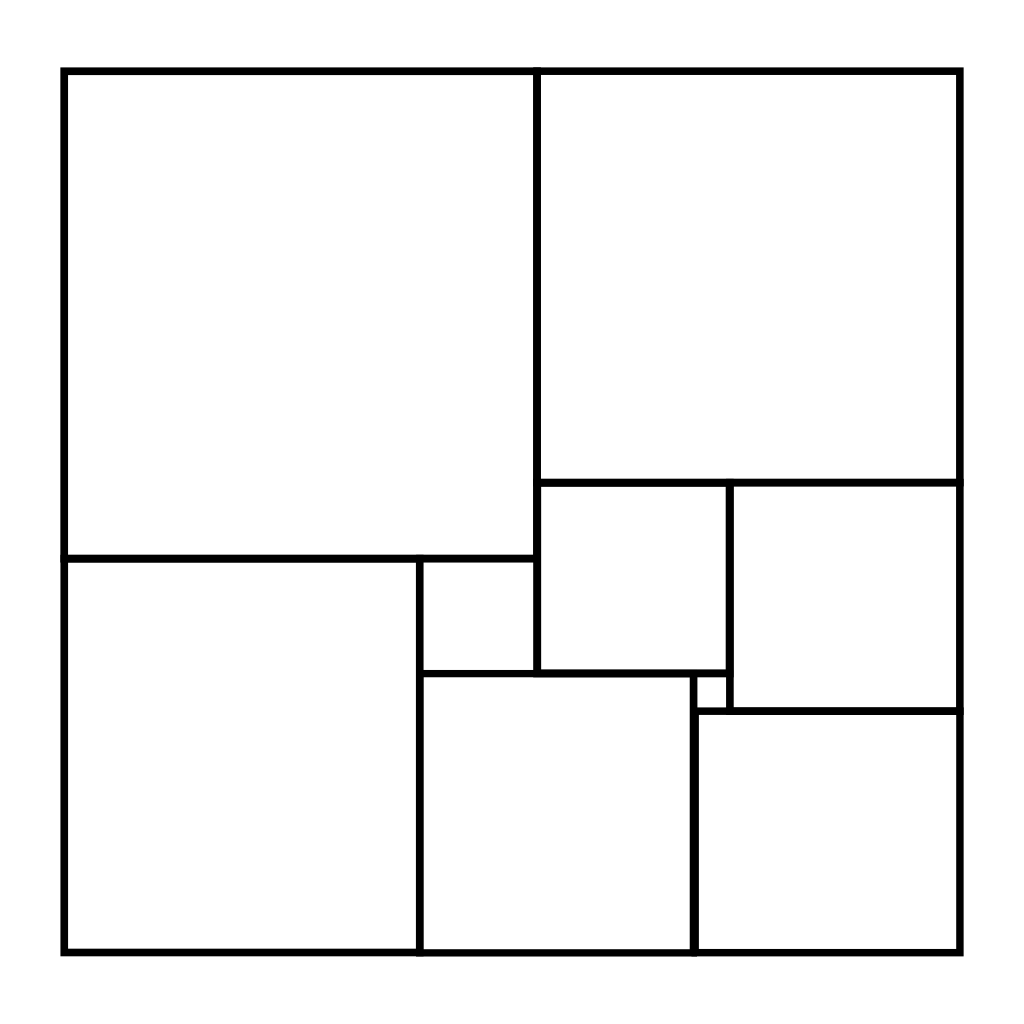
Si el quadrat més petit té costat $x$, i el seu veï més petit té costat $y$, és possible expressar els costats de tots els altres quadrats només fent servir $x$ i $y$.
El quadrat que hi ha a la dreta del quadrat més petit té costat que és la suma dels costats dels quadrats que hi ha a la seva esquerra: $x+y$. El quadrat d'abaix de tot i a la dreta té costat que és la suma dels costats del seus veïns per sobre: $x+(x+y) = 2x+y$. El quadrat de dalt de tot i a la dreta té costat $(x+y) + y= x+2y$. Continuant així podem trobar els costats de tots els quadrats en funció de $x$ i $y$. Per a l'últim quadrat tindrem dues expressions diferents que, junt amb l'alçada del rectangle, ens poden ajudar a trobar $x$ i $y$.
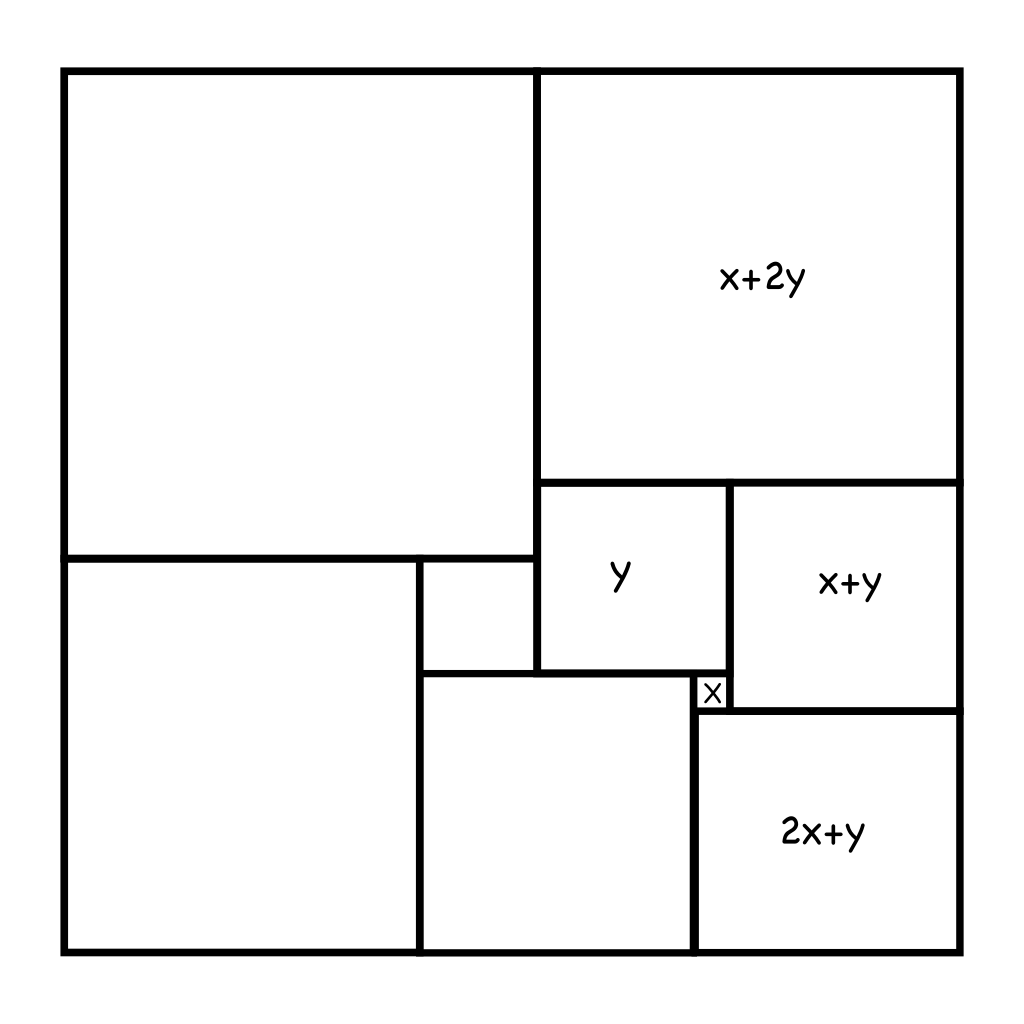
Si el quadrat més petit de tots té costat $x$, i el seu veï més petit té costat $y$, és possible expressar els costats de tots els altres quadrats només fent servir $x$ i $y$.
El quadrat que hi ha a la dreta del més petit té costat que és la suma dels costats dels quadrats que té a la seva esquerra: $x+y$. El quadrat de baix de tot i a la dreta té costat que és la suma dels costats del seus veïns per sobre: $x+(x+y) = 2x+y$. El quadrat de dalt de tot i a la dreta té costat $(x+y) + y= x+2y$. El quadrat de baix de tot i al mig té costat $x + (2x+y) = 3x +y$.
Per trobar el costat del segon quadrat més petit podem sumar els costat dels dos quadrats de baix i restar els costats dels dos quadrats a la seva dreta (vegeu la figura). El resultat és: $$ (2x+y) + (3x+y) - (x+y) - y = 5x + 2y - x - y - y = 4x.$$
El costat del quadrat de baix de tot i a l'esquerra és la suma dels costats dels dos veïns a la seva dreta: $4x + (3x+y) = 7x + y.$ Finalment, podem trobar el costats del quadrat de dalt de tot i a l'esquerra de dues maneres diferents: primer, sumant els costats dels seus veïns de baix: $7x+y +4x = 11x+y$, i segon, sumant els costats del quadrats que té a la dreta i restant el costat del quadrat del mig: $(x+2y) + y - (4x) = 3y - 3x.$
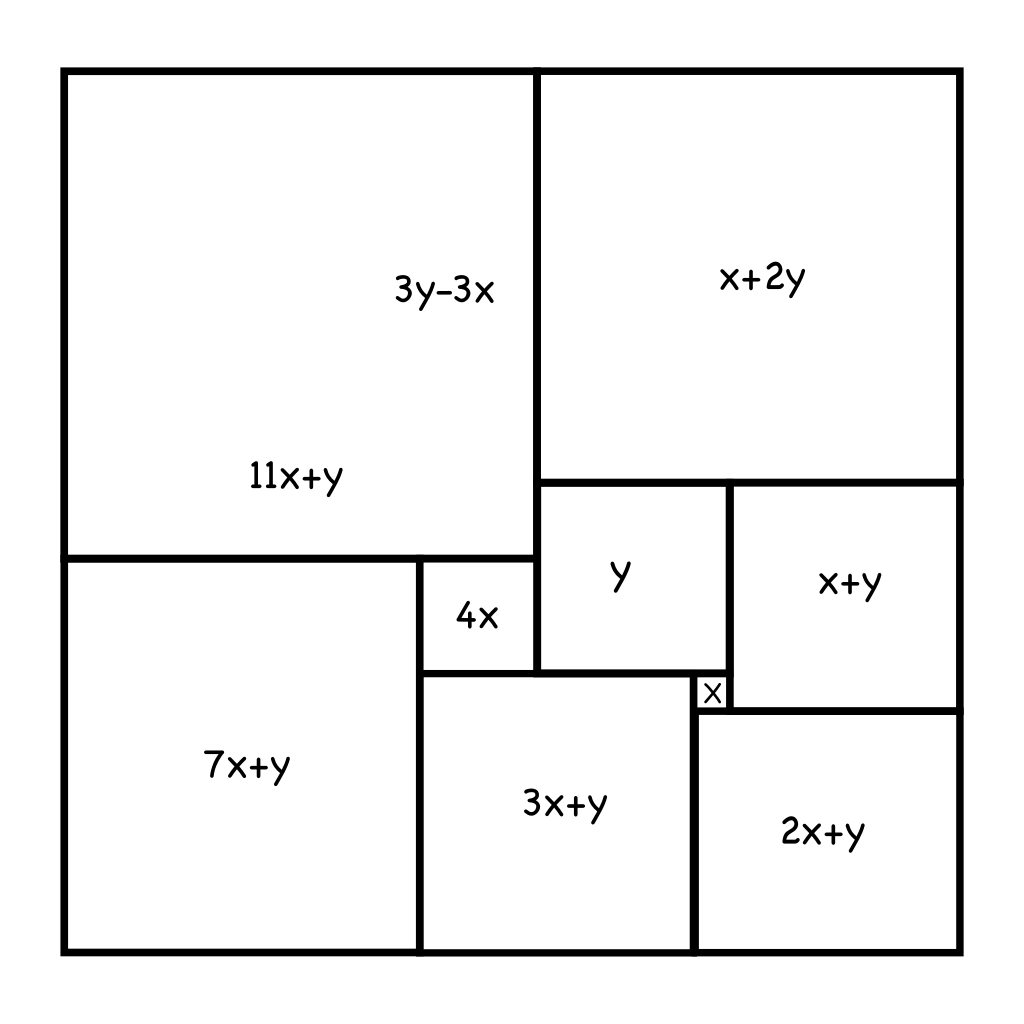
Tenim dues expressions per al quadrat de dalt de tot a l'esquerra. Per tant, podem concloure que $3y-3x=11x+y$. Sumem $3x$ als dos costats de l'equació i queda $3y = 14x + y$. Restem $y$ als dos costats de l'equació i queda $2y = 14x$. Dividim els dos costats entre dos i queda $y=7x$.
Finalment, l'alçada del rectangle és $$(7x+y) + (11x + y) = 18x + 2y.$$ Ja sabem que $y=7x$ i per tant l'alçada és $$18x + 2y = 18x + 2 \cdot 7x = 18x + 14 x = 32x.$$ Ens diuen que l'alçada és $32$ i per tant podem concloure que $x=1$ i $y=7$. Ja podem substituir aquests valors per trobar els costats de tots els $9$ quadrats.
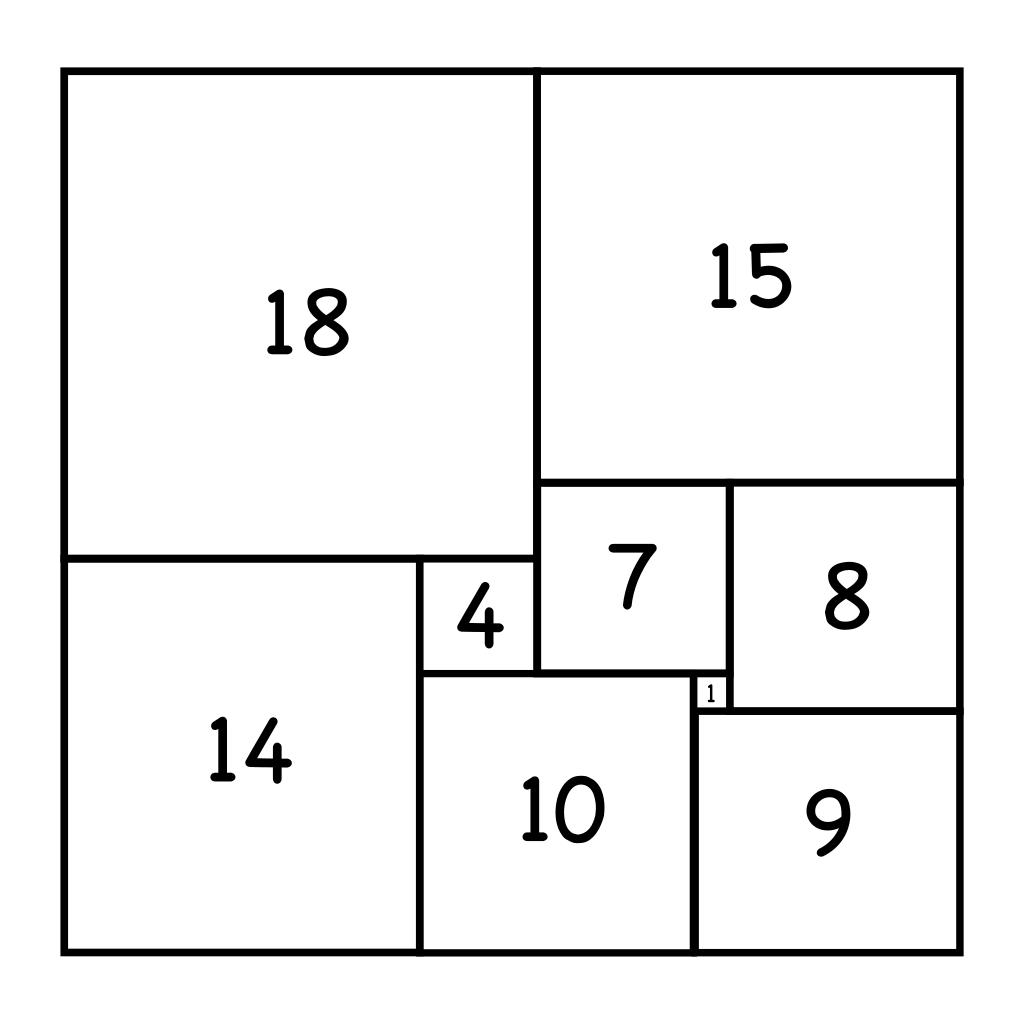 Sumant els costats dels quadrats de baix trobem que l'amplada del rectangle és $14+10+9 = \boxed{33}$.
Sumant els costats dels quadrats de baix trobem que l'amplada del rectangle és $14+10+9 = \boxed{33}$.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | jaquerol | jaquerol | 3 d’abril de 2021 a les 10:28 | 03/04/2021 |
| Or | marcsubirats | marcsubirats | 3 d’abril de 2021 a les 15:44 | 03/04/2021 |
| Or | paucamarillas | paucamarillas | 14 d’abril de 2021 a les 14:27 | 14/04/2021 |
| Or | Pol14 | Pol14 | 14 d’abril de 2021 a les 14:49 | 14/04/2021 |
| Or | David07 | David07 | 14 d’abril de 2021 a les 14:51 | 14/04/2021 |
| Or | Mariorizea | Mariorizea | 14 d’abril de 2021 a les 14:51 | 14/04/2021 |
| Or | Guillemayet | Guillemayet | 14 d’abril de 2021 a les 14:55 | 14/04/2021 |
| Or | martinos | martinos | 21 d’abril de 2021 a les 17:24 | 21/04/2021 |
| Or | JoanaFolia | JoanaFolia | 24 d’abril de 2021 a les 16:13 | 24/04/2021 |
| Xocolata | megawarret... | megawarret3000 | 14 d’abril de 2021 a les 14:24 | 14/04/2021 |
| Xocolata | Mar14 | Mar14 | 30 d’abril de 2021 a les 22:30 | 30/04/2021 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Hiperboloide | Hiperboloide | 1 d’abril de 2021 a les 11:56 | 01/04/2021 |
| Or | PACOVES | PACOVES | 2 d’abril de 2021 a les 18:57 | 02/04/2021 |
| Or | arakelov | arakelov | 2 d’abril de 2021 a les 20:17 | 02/04/2021 |
| Or | JABorrás | JABorrás | 3 d’abril de 2021 a les 5:29 | 03/04/2021 |
| Or | montserrat... | montserrat.muria | 3 d’abril de 2021 a les 11:22 | 03/04/2021 |
| Or | HFOLIACOTS | HFOLIACOTS | 24 d’abril de 2021 a les 14:36 | 24/04/2021 |
| Or | rsempere | rsempere | 26 d’abril de 2021 a les 12:04 | 26/04/2021 |
| Or | AlexandreR... | AlexandreRosales | 28 d’abril de 2021 a les 20:05 | 28/04/2021 |
| Or | Alexia2005 | Alexia2005 | 30 d’abril de 2021 a les 11:41 | 30/04/2021 |
| Plata | SoniaPC | SoniaPC | 5 d’abril de 2021 a les 23:24 | 05/04/2021 |
| Bronze | Pintor | Pintor | 14 d’abril de 2021 a les 14:49 | 14/04/2021 |
