La Martina ha dibuixat un $n$-àgon regular, és a dir, un polígon amb $n$ costats iguals. L'Oriol vol saber quants costats té, però ella només li respon el següent
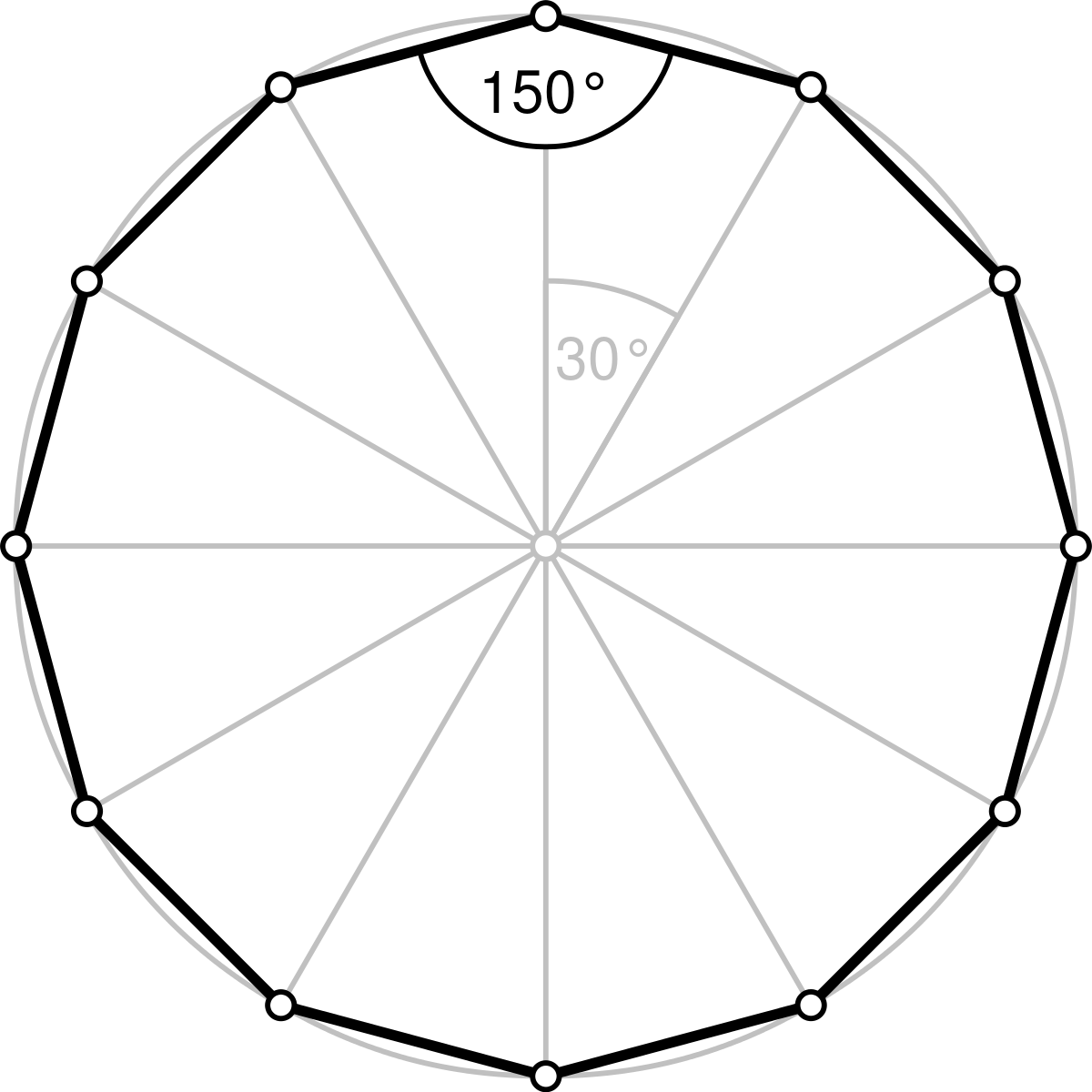
$\quad$ Els angles interiors del meu polígon valen $150^{\circ}$.
Amb aquesta informació, saps dir quant val $n$? És a dir, quants costats té el polígon de la Martina?
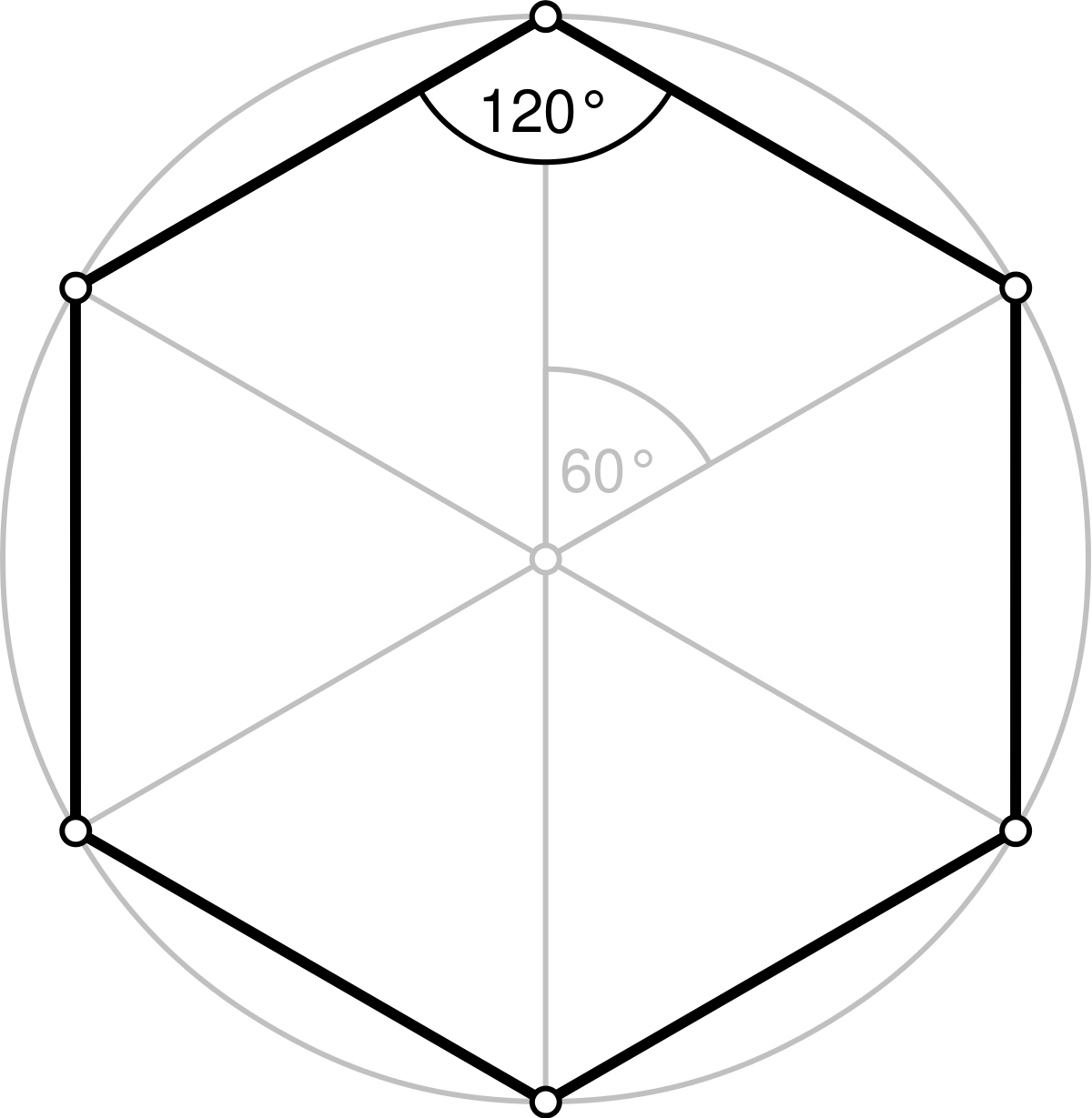
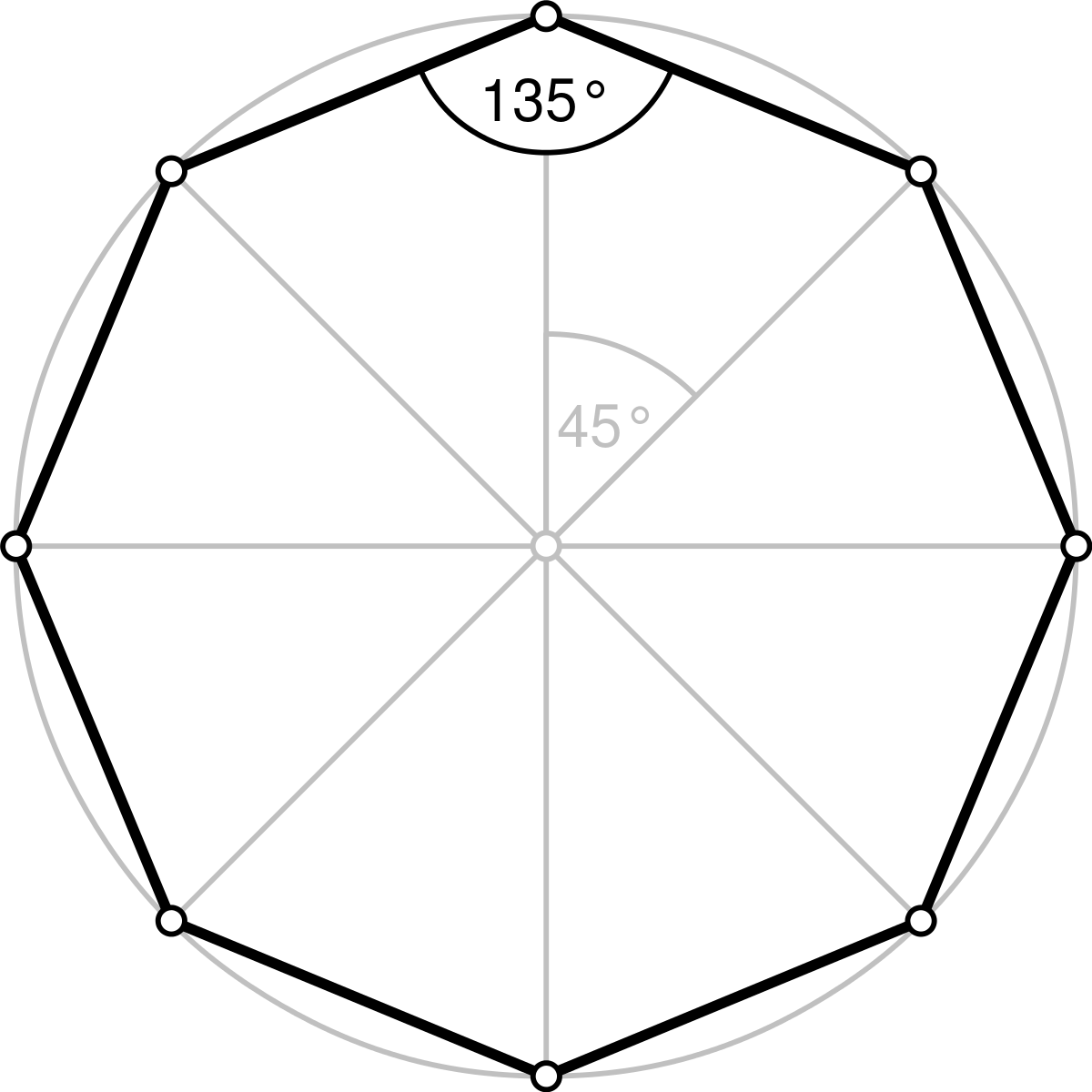
Nota: Per exemple, en un hexàgon regular ($6$ costats) l'angle interior val $120^{\circ}$. O per exemple, en un octàgon regular ($8$ costats), val $135^{\circ}$.
 $\quad \quad$
$\quad \quad$
Per trobar l'angle interior d'un polígon regular en general, primer de tot hem de veure que podem dividir el polígon en triangles iguals, unint els vèrtexs amb el centre. Raonem primer per a un heptàgon
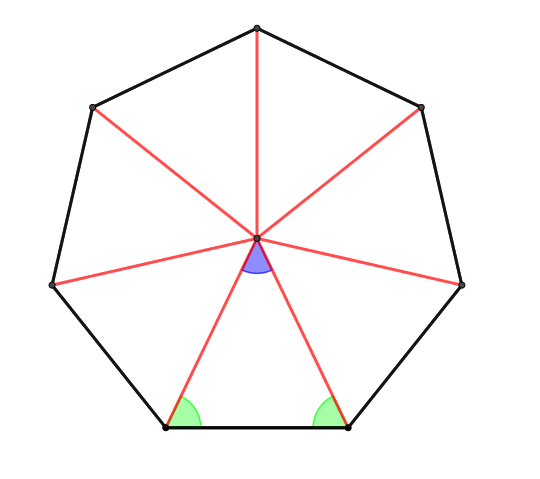
Ara, aquí és clar que l'angle blau és $1/7$ part de l'angle central, que val $360^{\circ}$ tot, és a dir $$ \textcolor{blue}{\angle Blau} = \frac{360^{\circ}}{7} $$
Aleshores, com el triangles dibuixats són isòsceles, els angles verds són iguals i podem veure que valen $$ 180^{\circ} = \textcolor{blue}{\angle Blau} + \textcolor{LimeGreen}{\angle Verd} +\textcolor{LimeGreen}{\angle Verd} \quad \Longrightarrow \quad \textcolor{LimeGreen}{\angle Verd} = \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{7} )$$
Llavors, l'angle interior de l'heptàgon és precisament dos cops l'angle verd. En conclusió, l'angle interior de l'heptàgon val $$ \angle \text{heptàgon} = 2\textcolor{LimeGreen}{\angle Verd} = 2 \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{7} ) = 180^{\circ} - \frac{360^{\circ}}{7}$$
Sabries calcular ara l'angle interior d'un polígon amb $n$ costats?
Si calculem per a un polígon regular de $n$ costats, obtindrem que l'angle interior és $$ \textcolor{blue}{\angle Blau} = \frac{360^{\circ}}{n} \quad \Longrightarrow \quad \textcolor{LimeGreen}{\angle Verd} = \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{n} ) \quad \Longrightarrow \quad \angle n\text{-àgon} = 180^{\circ}- \frac{360^{\circ}}{n}$$
Per tant, quant val $n$?
Anem a calcular quant val l'angle interior d'un polígon regular de $n$ costats.
Primer de tot, hem de veure que podem dividir el polígon en triangles iguals, unint els vèrtexs amb el centre. Per veure-ho clar, raonem primer per a un heptàgon ($7$ costats):

Ara, aquí és clar que l'angle blau és $1/7$ part de l'angle central, que val $360^{\circ}$ tot, és a dir $$ \textcolor{blue}{\angle Blau} = \frac{360^{\circ}}{7} $$
Aleshores, com el triangles dibuixats són isòsceles, els angles verds són iguals i podem veure que valen $$ 180^{\circ} = \textcolor{blue}{\angle Blau} + \textcolor{LimeGreen}{\angle Verd} +\textcolor{LimeGreen}{\angle Verd} \quad \Longrightarrow \quad \textcolor{LimeGreen}{\angle Verd} = \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{7} )$$
Llavors, l'angle interior de l'heptàgon és precisament dos cops l'angle verd. En conclusió, l'angle interior de l'heptàgon val $$ \angle \text{heptàgon} = 2\textcolor{LimeGreen}{\angle Verd} = 2 \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{7} ) = 180^{\circ} - \frac{360^{\circ}}{7}$$
Si fem això per un polígon regular de $n$ costats, obtindrem que l'angle interior és $$ \textcolor{blue}{\angle Blau} = \frac{360^{\circ}}{n} \quad \Longrightarrow \quad \textcolor{LimeGreen}{\angle Verd} = \frac{1}{2} ( 180^{\circ} - \frac{360^{\circ}}{n} ) \quad \Longrightarrow \quad \angle n\text{-àgon} = 180^{\circ}- \frac{360^{\circ}}{n}$$
Si la Martina diu que l'angle interior del seu polígon regular és de $150^{\circ}$, podem aïllar $n$ com $$ 150^{\circ} = 180^{\circ} - \frac{360^{\circ}}{n} \quad \Longrightarrow \quad n = \frac{360^{\circ}}{30^{\circ}} = 12 $$
En conclusió, el polígon de la Martina té $\boxed{n=12 \text{ costats}}$.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | mar2 | mar2 | 1 de març de 2021 a les 10:09 | 01/03/2021 |
| Or | EloiOrigami | EloiOrigami | 1 de març de 2021 a les 10:49 | 01/03/2021 |
| Or | rubenvinaros | rubenvinaros | 1 de març de 2021 a les 17:03 | 01/03/2021 |
| Or | martinos | martinos | 1 de març de 2021 a les 19:21 | 01/03/2021 |
| Or | Pol14 | Pol14 | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Or | paucamarillas | paucamarillas | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Or | David07 | David07 | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Or | Mariorizea | Mariorizea | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Or | jaquerol | jaquerol | 3 de març de 2021 a les 16:00 | 03/03/2021 |
| Or | JoanaFolia | JoanaFolia | 3 de març de 2021 a les 20:44 | 03/03/2021 |
| Or | malbaiges1... | malbaiges19@inspgirona.cat | 25 de març de 2021 a les 21:27 | 25/03/2021 |
| Or | Blanca | Blanca | 31 de març de 2021 a les 9:59 | 31/03/2021 |
| Or | Leire | Leire | 31 de març de 2021 a les 10:43 | 31/03/2021 |
| Plata | HctorCifre | HctorCifre | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Plata | Guillemayet | Guillemayet | 3 de març de 2021 a les 14:35 | 03/03/2021 |
| Plata | Mar14 | Mar14 | 30 de març de 2021 a les 23:25 | 30/03/2021 |
| Xocolata | megawarret... | megawarret3000 | 3 de març de 2021 a les 14:35 | 03/03/2021 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | JABorrás | JABorrás | 1 de març de 2021 a les 4:55 | 01/03/2021 |
| Or | Guillem27 | Guillem27 | 1 de març de 2021 a les 9:37 | 01/03/2021 |
| Or | ORIOL27 | ORIOL27 | 1 de març de 2021 a les 9:40 | 01/03/2021 |
| Or | Marc_Vitales | Marc_Vitales | 1 de març de 2021 a les 9:41 | 01/03/2021 |
| Or | jana07 | jana07 | 1 de març de 2021 a les 9:42 | 01/03/2021 |
| Or | tmillan | tmillan | 1 de març de 2021 a les 11:24 | 01/03/2021 |
| Or | montserrat... | montserrat.muria | 1 de març de 2021 a les 16:15 | 01/03/2021 |
| Or | Alexia2005 | Alexia2005 | 1 de març de 2021 a les 17:27 | 01/03/2021 |
| Or | Nomarolbap | Nomarolbap | 2 de març de 2021 a les 18:51 | 02/03/2021 |
| Or | AlexandreR... | AlexandreRosales | 3 de març de 2021 a les 16:27 | 03/03/2021 |
| Or | Ana.11.17 | Ana.11.17 | 4 de març de 2021 a les 21:41 | 04/03/2021 |
| Or | AlvaroSalon | AlvaroSalon | 6 de març de 2021 a les 20:25 | 06/03/2021 |
| Or | Marta1876 | Marta1876 | 27 de març de 2021 a les 7:43 | 27/03/2021 |
| Or | sergioRG | sergioRG | 28 de març de 2021 a les 13:18 | 28/03/2021 |
| Or | Diegosal | Diegosal | 29 de març de 2021 a les 12:32 | 29/03/2021 |
| Or | evmogi | evmogi | 31 de març de 2021 a les 21:27 | 31/03/2021 |
| Bronze | Pintor | Pintor | 3 de març de 2021 a les 14:35 | 03/03/2021 |
