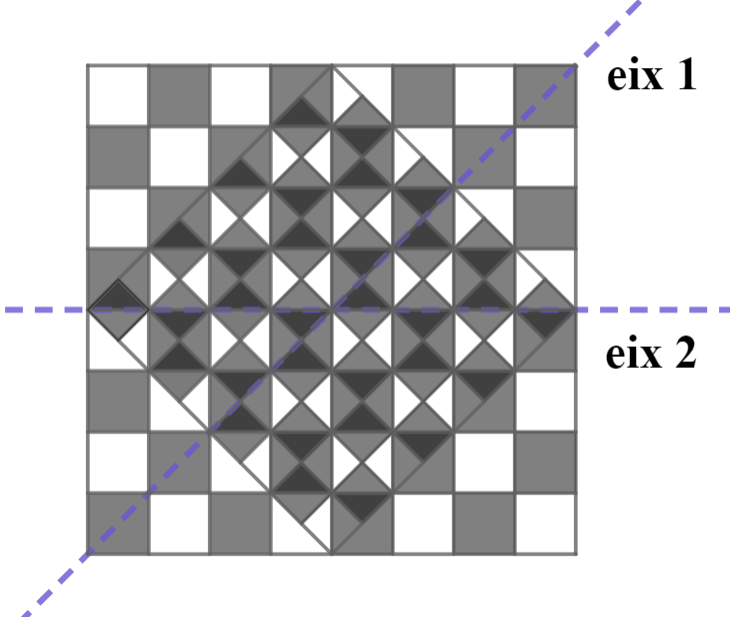
Hem agafat dos taulers d'escacs translúcids, de mides diferents i els hem superposat tal com en la figura. Sabent que el costat del tauler gran és 20, quina és l'àrea total de la regió on es superposen quadrats negres d'ambdòs taulers?

Seria diferent la resposta si ens demanessin per l'àrea on es superposen quadrats blancs del tauler gran sobre negres del petit? O blancs dels dos taulers? Aquest problema es pot ressoldre sense fer pràcticament cap càlcul, igual que si ens haguessin demanat l'àrea de només els quadrats blancs del tauler gran.
L'àrea on es superposen quadrats negres dels dos taulers és exactament una quarta part de l'àrea del tauler petit; i l'àrea del tauler petit és una fracció molt senzilla de la del gran.
Prova a separar el quadrat gran en 4 quadrants (amb un segment horitzontal i un altre vertical que passin pel centre).
En primer lloc, adonem-mos que la figura en qüestió té diverses simetries. Adonem-nos que tota l'àrea superposada és del tipus Blanc-Blanc, Blanc-Negre, Negre-Blanc o Negre-Negre (on el primer color és el del quadrat del tauler gran i el segon el del tauler petit).
Si girem els taulers al voltant d'un eix diagonal, com que el quadrat gran és simètric respecte a aquest eix i en el petit estem intercanviant la regió blanca amb la negra, estarem intercanviant les regions Blanc-Blanc amb Blanc-Negre i les regions Negre-Blanc amb Negre-Negre. Com que podem intercanviar les regions Blanc-Blanc i Blanc-Negre d'aquesta manera, deu ser que tenen la mateixa àrea; i el mateix amb les regions Negre-Blanc i Negre-Negre.
Si girem els taulers respecte d'un eix horitzontal, de nou un dels taulers es quedarà igual (el petit) i en l'altre (el gran) intercanviarem les regions blanques i les negres. Així que estarem intercanviant Blanc-Blanc amb Negre-Blanc i Blanc-Negre amb Negre-Negre.
En resum, tenim que: $$ Àrea[BB] = Àrea[BN]=Àrea[NB]=Àrea[NN]$$
Així que l'àrea de la regió on es superposen els quadrats negres dels dos és una quarta part de l'àrea del quadrat petit.
Una altra d'arribar a la mateixa conclusió és comptar el nombre de triangles os es superposen dos quadrats negres. Hi ha $32$, tots de la mateixa mida. Com que el tauler petit està format per $8\times 8 = 64$ quadrats, cadascun separat en $2$ triangles, l'àrea del tauler petit és $64\times 2 = 128$, és a dir, $4$ cops l'àrea de la regió on es superposen quadrats negres.
A més, si subdividim el tauler gran en quatre quadrants, queda clar que l'àrea del quadrat petit és la meitat que la del gran. És el cas en cada quadrant, així que és el cas en tot el tauler.
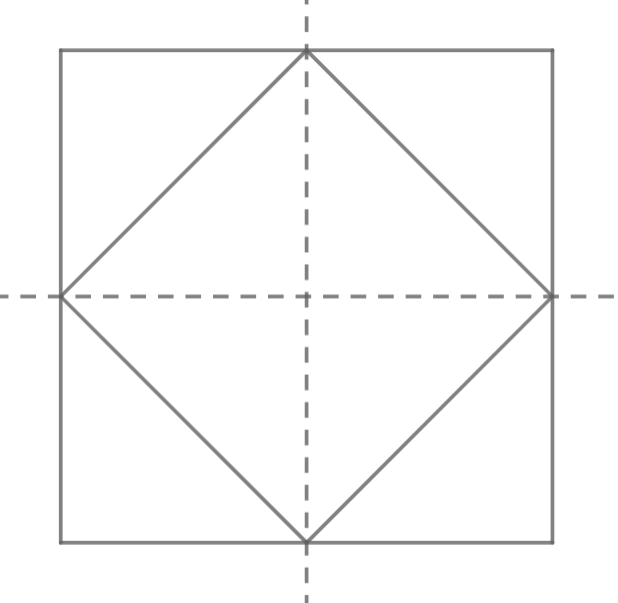
La del gran és $20\cdot 20=400$, així que la del petit és $400/2=200$ i la de l'àrea on es superposen quadrats negre sobre negre és $200/4=50$.
Així que la resposta és $\boxed{50}$.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | SansUDR | SansUDR | 7 de desembre de 2022 a les 14:43 | 07/12/2022 |
| Or | Hugotarugo | Hugotarugo | 7 de desembre de 2022 a les 14:44 | 07/12/2022 |
| Or | Nachulus | Nachulus | 7 de desembre de 2022 a les 14:44 | 07/12/2022 |
| Or | edwesley | edwesley | 7 de desembre de 2022 a les 14:46 | 07/12/2022 |
| Or | Hypergg2000 | Hypergg2000 | 9 de desembre de 2022 a les 23:40 | 09/12/2022 |
| Or | martinos | martinos | 30 de desembre de 2022 a les 21:38 | 30/12/2022 |
| Plata | oripq | oripq | 7 de desembre de 2022 a les 14:44 | 07/12/2022 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | montserrat... | montserrat.muria | 1 de desembre de 2022 a les 18:29 | 01/12/2022 |
| Or | JABorrás | JABorrás | 1 de desembre de 2022 a les 23:58 | 01/12/2022 |
| Or | Hiperboloide | Hiperboloide | 2 de desembre de 2022 a les 9:25 | 02/12/2022 |
| Or | arakelov | arakelov | 4 de desembre de 2022 a les 10:24 | 04/12/2022 |
| Or | tremar | tremar | 7 de desembre de 2022 a les 14:53 | 07/12/2022 |
| Or | mellamanhy | mellamanhy | 21 de desembre de 2022 a les 18:13 | 21/12/2022 |
| Or | jaquerol | jaquerol | 31 de desembre de 2022 a les 22:14 | 31/12/2022 |
| Plata | Toni-michicú | Toni-michicú | 5 de desembre de 2022 a les 11:31 | 05/12/2022 |
| Xocolata | fakeone | fakeone | 9 de desembre de 2022 a les 23:35 | 09/12/2022 |
