En Mario està organitzant un sopar amb els seus amics, i està cuinant una pizza molt gran. Voldrà tallar la pizza en uns quants trossos (no necessàriament iguals!), per poder repartir-los entre els seus amics. Ara bé, en Mario és molt gandul, i vol aconseguir el màxim nombre de trossos fent com menys talls possible, i fent només talls en línia recta.
Per exemple, si només fes un tall, només pot aconseguir dividir la pizza en $2$ trossos.
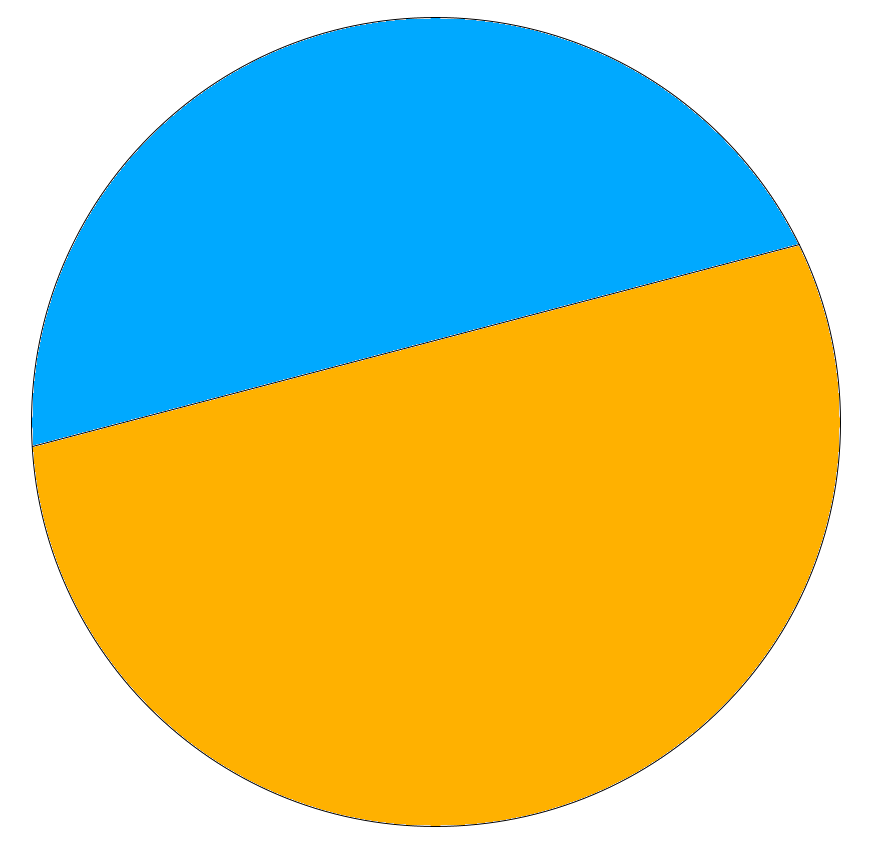
Si fes dos talls, pot aconseguir $4$ trossos.
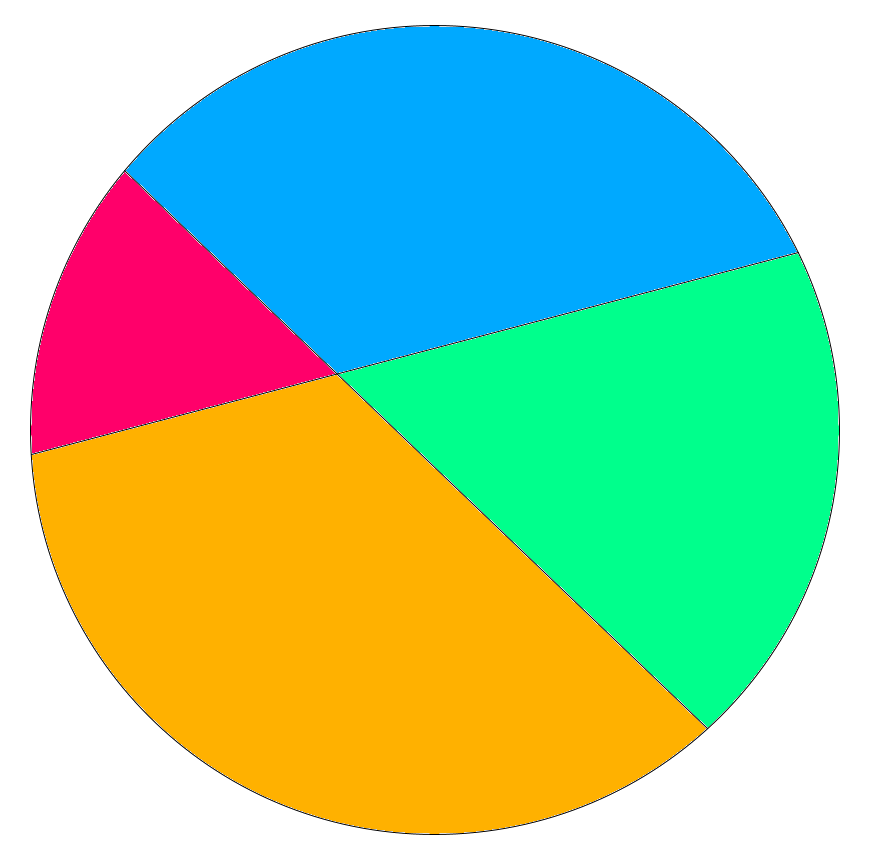
Si fes tres talls, podria aconseguir màxim $7$ trossos.
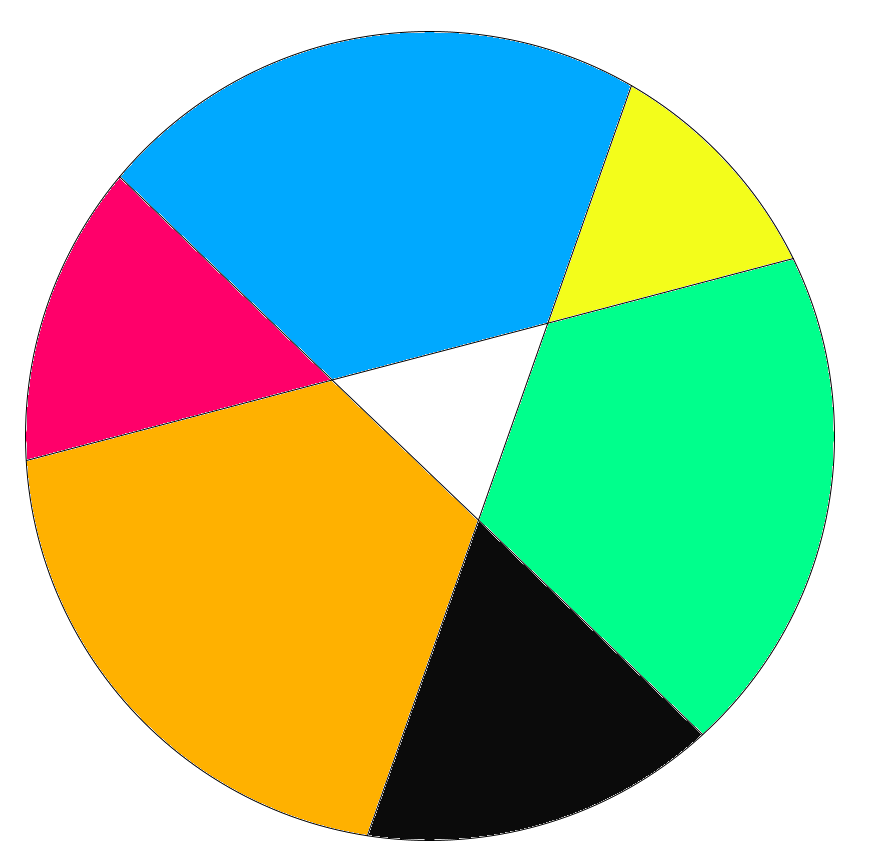
En quants trossos pot dividir la pizza en Mario, si només fa $10$ talls?
Fixa't en quants trossos nous apareixen amb cada tall.
Concretament, el segon tall ens dona $4-2=2$ trossos més, el tercer tall ens dona $7-4=3$ trossos més... Veus quin patró segueix?
En general, el tall $n$-èssim ens dona $n$ trossos nous, com a molt. Donada una configuració on ja hem fet $n-1$ talls

Com que els talls que fem són línies rectes, només poden tallar als altres talls ja existents en un únic punt cada vegada.
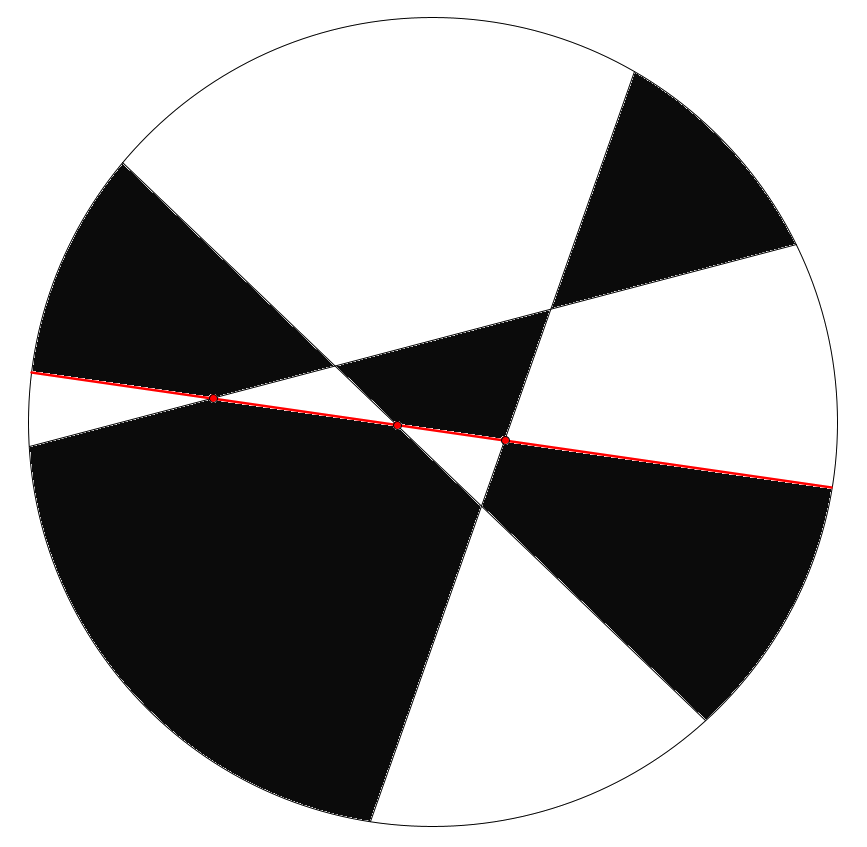
Per tant, es crearan $n-1+1=n$ regions noves. El $n-1$ surt de que per cada tall entre rectes generarà una nova regió, amb un $+1$ addicional que ve de l'última regió que també es converteix en dues.
Per tant, podem calcular el màxim nombre de trossos segons quants talls fem com
$ \qquad 1 \text{ tall} \longrightarrow 2 \text{ trossos} $
$ \qquad 2 \text{ tall} \longrightarrow 2+{\color{red} 2} = 4 \text{ trossos} $
$ \qquad 3 \text{ tall} \longrightarrow 2+2+{\color{red} 3} = 7 \text{ trossos} $
$ \qquad \quad \vdots $
Primer de tot ens fixem en quants trossos nous apareixen amb cada tall.
Concretament, el segon tall ens dona $4-2=2$ trossos més, el tercer tall ens dona $7-4=3$ trossos més... En general, el tall $n$-èssim ens dona $n$ trossos nous, com a molt.
Ho podem provar gràficament, donada una configuració on ja hem fet $n-1$ talls

Com que els talls que fem són línies rectes, només poden tallar als altres talls ja existents en un únic punt cada vegada.

Per tant, es crearan $n-1+1=n$ regions noves. El $n-1$ surt de que per cada tall entre rectes generarà una nova regió, amb un $+1$ addicional que ve de l'última regió que també es converteix en dues.
Per tant, podem calcular el màxim nombre de trossos segons quants talls fem com
$ \qquad 1 \text{ tall} \longrightarrow 2 \text{ trossos} $
$ \qquad 2 \text{ tall} \longrightarrow 2+{\color{red} 2} = 4 \text{ trossos} $
$ \qquad 3 \text{ tall} \longrightarrow 2+2+{\color{red} 3} = 7 \text{ trossos} $
$ \qquad \quad \vdots $
$ \qquad 10 \text{ talls} \longrightarrow 2+2+3+4+5+6+7+8+9+{\color{red} 10} = 56 \text{ trossos} $
És a dir, amb $10$ talls en Mario podrà aconseguir $\boxed{56 \text{ trossos de pizza}}$.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Nachulus | Nachulus | 2 de febrer de 2022 a les 14:17 | 02/02/2022 |
| Or | Hypergg2000 | Hypergg2000 | 2 de febrer de 2022 a les 15:37 | 02/02/2022 |
| Or | anabel | anabel | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Or | ferranfatsini | ferranfatsini | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Or | Jj | Jj | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Or | EloiOrigami | EloiOrigami | 3 de febrer de 2022 a les 19:28 | 03/02/2022 |
| Or | Érika12 | Érika12 | 9 de febrer de 2022 a les 14:17 | 09/02/2022 |
| Or | Asoler | Asoler | 19 de febrer de 2022 a les 10:57 | 19/02/2022 |
| Plata | @el_bicho_cr7 | @el_bicho_cr7 | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Plata | mainclaaaa | mainclaaaa | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Plata | Ekain008 | Ekain008 | 11 de febrer de 2022 a les 16:00 | 11/02/2022 |
| Bronze | sabn | sabn | 2 de febrer de 2022 a les 14:36 | 02/02/2022 |
| Bronze | SansUDR | SansUDR | 2 de febrer de 2022 a les 14:50 | 02/02/2022 |
| Bronze | mikelet20097 | mikelet20097 | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Bronze | scastello2... | scastello20@instpamies.cat | 24 de febrer de 2022 a les 17:05 | 24/02/2022 |
| Bronze | MAMG | MAMG | 24 de febrer de 2022 a les 18:00 | 24/02/2022 |
| Xocolata | evg | evg | 2 de febrer de 2022 a les 14:36 | 02/02/2022 |
| Xocolata | mj | mj | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Xocolata | martinos | martinos | 19 de febrer de 2022 a les 15:22 | 19/02/2022 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | arakelov | arakelov | 1 de febrer de 2022 a les 7:30 | 01/02/2022 |
| Or | luca.passo... | luca.passolini2017 | 1 de febrer de 2022 a les 9:09 | 01/02/2022 |
| Or | montserrat... | montserrat.muria | 1 de febrer de 2022 a les 9:37 | 01/02/2022 |
| Or | Monroe | Monroe | 1 de febrer de 2022 a les 20:20 | 01/02/2022 |
| Or | rsempere | rsempere | 1 de febrer de 2022 a les 20:57 | 01/02/2022 |
| Or | tmillan | tmillan | 2 de febrer de 2022 a les 9:15 | 02/02/2022 |
| Or | Hiperboloide | Hiperboloide | 3 de febrer de 2022 a les 7:44 | 03/02/2022 |
| Or | Motxo | Motxo | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Or | Pajarito | Pajarito | 3 de febrer de 2022 a les 14:22 | 03/02/2022 |
| Or | jaquerol | jaquerol | 5 de febrer de 2022 a les 18:37 | 05/02/2022 |
| Or | JABorrás | JABorrás | 5 de febrer de 2022 a les 22:34 | 05/02/2022 |
| Or | Maria65 | Maria65 | 6 de febrer de 2022 a les 11:39 | 06/02/2022 |
| Or | francesccid | francesccid | 14 de febrer de 2022 a les 11:07 | 14/02/2022 |
| Or | Marcsubira... | Marcsubirats01 | 14 de febrer de 2022 a les 11:08 | 14/02/2022 |
| Or | Alexia2005 | Alexia2005 | 28 de febrer de 2022 a les 18:56 | 28/02/2022 |
| Plata | Alejandro | Alejandro | 1 de febrer de 2022 a les 17:27 | 01/02/2022 |
| Plata | Marta1876 | Marta1876 | 1 de febrer de 2022 a les 20:13 | 01/02/2022 |
| Plata | jaiopti99 | jaiopti99 | 2 de febrer de 2022 a les 14:18 | 02/02/2022 |
| Plata | fakeone | fakeone | 2 de febrer de 2022 a les 15:21 | 02/02/2022 |
| Bronze | Cire | Cire | 8 de febrer de 2022 a les 22:19 | 08/02/2022 |
| Bronze | Francesca2 | Francesca2 | 14 de febrer de 2022 a les 22:59 | 14/02/2022 |
