Sobre una circumferència tracem $5$ punts diferents, i hi dibuixem tots els segments possibles unint parelles d'aquests punts.
Quants triangles podem comptar, com a màxim, en el dibuix resultant?
És més senzill distingir els triangles segons el nombre de vèrtexs que tinguin sobre la circumferència.
Els triangles amb tots els vèrtexs sobre la circumferència surten de triar tres punts d'entre els cinc punts possibles, per tant, n'hi ha ${5\choose 3}=10$.
Els triangles amb dos vèrtexs sobre la circumferència i un interior es formen a partir d'unir els segments entre quatre punts

i n'apareixen quatre. Per tant, en tenim $4\cdot {5\choose 4} = 4\cdot 5 = 20$.
Quants n'hi ha amb només un vèrtex sobre la circumferència? I amb cap?
Els triangles amb un vèrtex sobre la circumferència i dos interiors es formen a partir d'unir els segments entre cinc punts
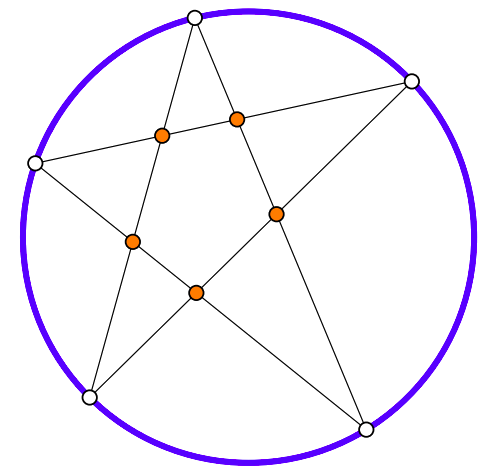
i n'apareixen cinc. Per tant, en tenim $5\cdot {5 \choose 5} = 5 \cdot 1 = 5$.
Per últim, veiem que no podem tenir triangles amb cap vèrtex sobre la circumferència, ja que allargant-ne els costats veiem que necessitaríem mínim sis punts, malgrat en tenim només cinc.
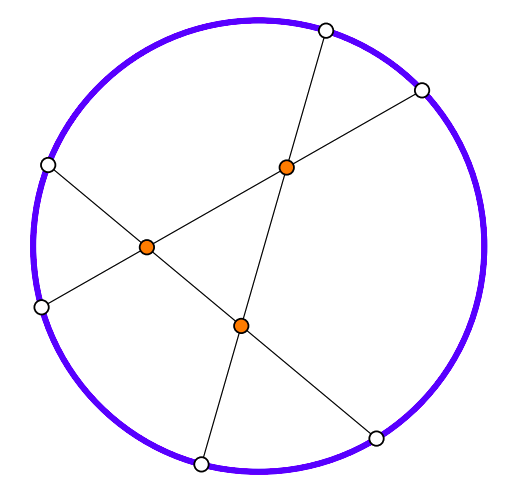
Per tant, quants n'hi ha en total?
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 4t d'ESO
Estudiants que cursen 4t d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Hypergg2000 | Hypergg2000 | 3 de juny de 2022 a les 16:45 | 03/06/2022 |
Classificació oberta
Usuaris que ja han superat
4t d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Plata | arakelov | arakelov | 1 de juny de 2022 a les 12:33 | 01/06/2022 |
| Plata | montserrat... | montserrat.muria | 1 de juny de 2022 a les 18:21 | 01/06/2022 |
| Plata | luca.passo... | luca.passolini2017 | 5 de juny de 2022 a les 18:07 | 05/06/2022 |
| Bronze | JABorrás | JABorrás | 13 de juny de 2022 a les 0:12 | 13/06/2022 |
| Xocolata | fakeone | fakeone | 3 de juny de 2022 a les 9:43 | 03/06/2022 |
