Considerem un quadrat de costat $1$ amb vèrtexos $A,B,C,D$. Sigui $S$ la regió formada pels punts $P$ que estan dins del quadrat (els costats i vèrtexos també compten) i tals que $AP^2+BP^2+CP^2+DP^2 \leq \frac{10}{3}$. Calculeu l’àrea de la regió $S$.
Doneu la vostra resposta com un número decimal arrodonit a dues xifres decimals. Per exemple, si l'àrea fos $2.617…$, responeu $2.62$.
Intenteu averiguar quina és la forma de la regió $S$; és la intersecció entre el quadrat i una figura arrodonida. Us ajudarà escriure la condició $AP^2+BP^2+CP^2+DP^2 \leq \frac{10}{3}$ en funció de les coordenades cartesianes del punt $P$.
I teniu en compte que hi han punts de fora del quadrat que satisfan la condició de desigualtat: $AP^2+BP^2+CP^2+DP^2 \leq \frac{10}{3}$
Utilitzant coordenades cartesianes es pot veure que la regió $S$ és la regió a l'interior de la corva blava següent:
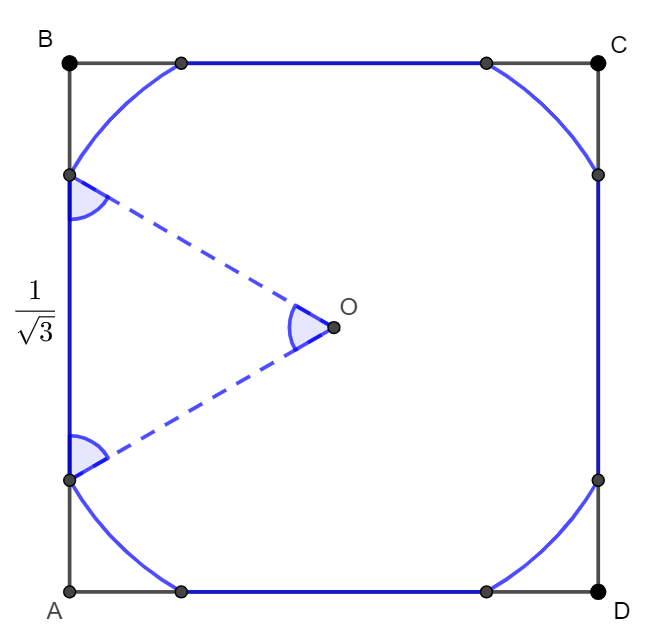
Aprofitant la distància del dibuix, el fet que els tres angles blaus són iguals i la simetria de la figura, subdividiu ara la regió $S$ en subregions de les que sigui més fàcil calcular l’àrea, com triangles i sectors circulars.
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data |
|---|
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | arakelov | arakelov | 1 de novembre de 2022 a les 9:27 | 01/11/2022 |
| Plata | JABorrás | JABorrás | 1 de novembre de 2022 a les 19:11 | 01/11/2022 |
| Plata | montserrat... | montserrat.muria | 3 de novembre de 2022 a les 17:27 | 03/11/2022 |
