Un cometa és un quadrilàter que té les dues diagonals perpendiculars. També s'anomenen quadrilàters ortodiagonals, però aquí els anomenarem cometes.
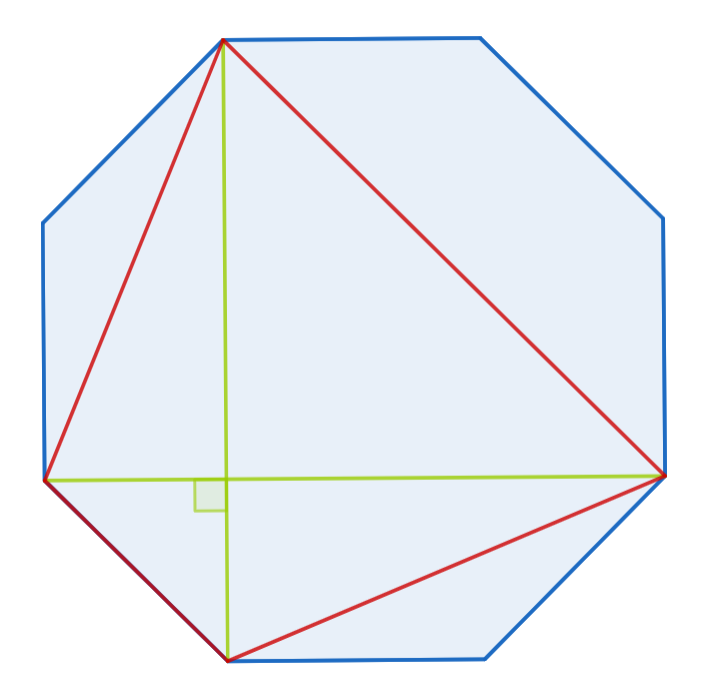
En Pere ha estat fent un taller de dibuixar estreles amb les diagonals de polígons regulars i se n'adona que de vegades les diagonals d'aquests polígons són perpendiculars, formant aleshores un cometa. En aquest cas, per exemple, com que les diagonals verdes són perpendiculars, el quadrilàter roig és cometa.
Amb les fotocòpies que té, una de cada polígon regular d'entre $3$ i $9$ costats, quina quantitat de cometes diferents podrà dibuixar?
NOTA: Un cometa i un altre que té la mateixa forma però està rotat respecte al primer no es consideren iguals. És a dir, volem la suma del nombre de grups de $4$ vèrtexs que donen un cometa per cada polígon regular d'entre $3$ i $9$ costats.
Sembla que els polígons de nombre senar de costats són molt diferents als de nombre parell de costats. En el senars no hi ha cap cometa i en els parells és fàcil calcular la quantitat de cometes que tenen una diagonal particular, és la quantitat de vèrtexs entre els dos extrems (anant pel camí més curt).
Els polígons de nombre senar de costats no donen cap cometa i en els polígons de nombre parell de costats podem trobar una fórmula general pel nombre de cometes en que participa un vèrtex qualsevol.
Sigui $n=2k$ el nombre de costats del polígon. Fixem un vèrtex $A$ i calculem la quantitat de cometes que tenen a $A$. Separant per casos en funció de quin sigui el vèrtex oposat, obtenim la quantitat $1+2+\cdots+(k-1)+1+2+\cdots+(k-2) = (k-1)^2$
Ara només ens falta fer la suma de la quantitat de cometes en que està cada vèrtex i dividir entre el nombre de vèrtexs que té cada cometa.
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data |
|---|
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | arakelov | arakelov | 27 d’octubre de 2022 a les 13:46 | 27/10/2022 |
| Plata | Oriol47 | Oriol47 | 2 d’octubre de 2022 a les 13:07 | 02/10/2022 |
| Xocolata | JABorrás | JABorrás | 4 d’octubre de 2022 a les 7:07 | 04/10/2022 |
| Xocolata | DJPIÑATA | DJPIÑATA | 9 d’octubre de 2022 a les 20:58 | 09/10/2022 |
