L'Anna ha estat jugant amb un tauler hexagonal i unes peces en forma de diamant que li han regalat pel seu aniversari. La graella és un hexàgon regular de costat 2 subdividit en triangles equilàters de costat 1 com en la figura:
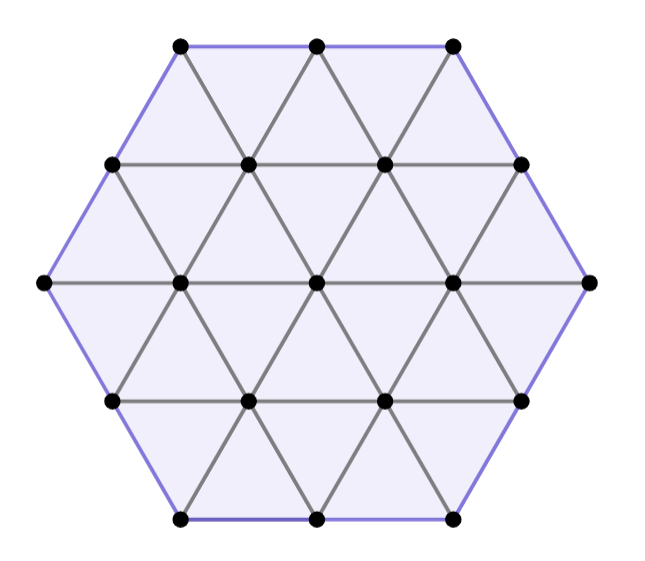
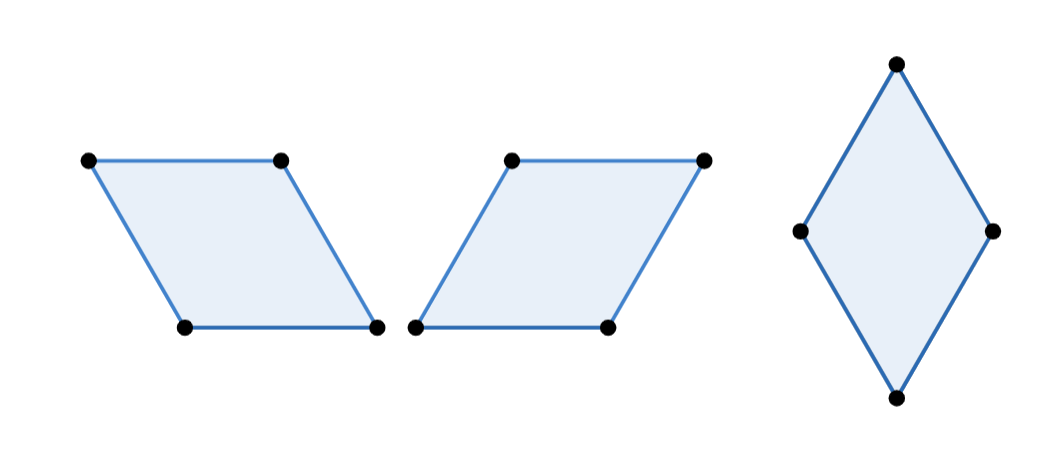
Les peces amb forma de diamant mesuren exactament el mateix que dos d'aquestes caselles amb forma de triangle equilàter i es poden posar recobrint dues caselles en horitzontal (com en els primers dos diagrames) o en vertical (com en l'últim):
Anna s'ha adonat que hi ha moltes maneres diferents de recobrir el tauler amb diamants (sense deixar forats ni que es solapin dues peces), així que s'ha proposat el repte d'omplir el tauler amb el mínim possible de diamants en vertical. Quin és aquest nombre mínim?
Es pot fer amb zero? No, perquè si subdivideixes l'hexàgon en $4$ files, en cada fila hi haurà un nombre senar de triangles, que no es poden cobrir completament perquè els diamants horitzontals recobreixen sempre exactament dos triangles de la mateixa fila. Com que aixó passa en totes les files, cal que en cada fila al menys una casella estigui coberta per un diamant vertical. Així que cal al menys 2. Es pot fer amb dos? Si ho fas amb dos, cal que un pertanyi a la primera i segona fila; i l'altre a la tercera i quarta fila. Pots fer-lo amb dos? I amb quatre?
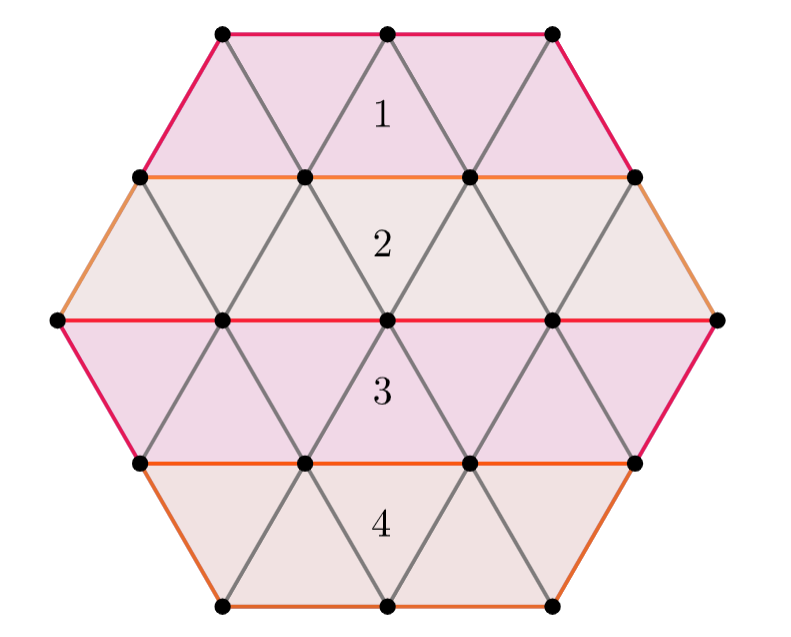
Tampoc es pot fer amb dos, perquè si ho intentes fer i com hem dit abans poses un diamant vertical que cobreixi la fila 1 i la 2, i un altre que cobreixi les files 3 i 4; trobaràs que les files 2 i 3 es queden separades en dues parts, però les dues tenen un nombre senar de caselles, així que en cada part cal al menys un diamant vertical. En total dos més, de manera que sabem que cal al menys 4 diamants verticals en total.
Així que només cal veure si amb 4 es pot. Intenta trobar-hi un exemple.
Fem una observació clau. Suposem que hem posat tots els diamants verticals en el tauler. Aleshores només queda recobrir la superfície restant amb diamants horitzontals. Per comoditat dividim el tauler en files horitzontals, de manera que cada diamant horitzontal cobreix dues caselles de la mateixa fila. Per tant els trossos de fila que havien quedat per recobrir deuen tenir un nombre parell de caselles.

Anem a posar els diamants verticals complint la condició que acabem de deduïr. Comencem per la fila 1. Com que té un nombre senar de caselles, cal que hi hagi al menys un diamant vertical. De fet, una vegada posem el diamant vertical la fila 1 només es pot omplir d'una manera, ja que ens trobem caselles que ja només tenen un veí que no està ocupat per un diamant. Així que la fila 1 té exactament un diamant.
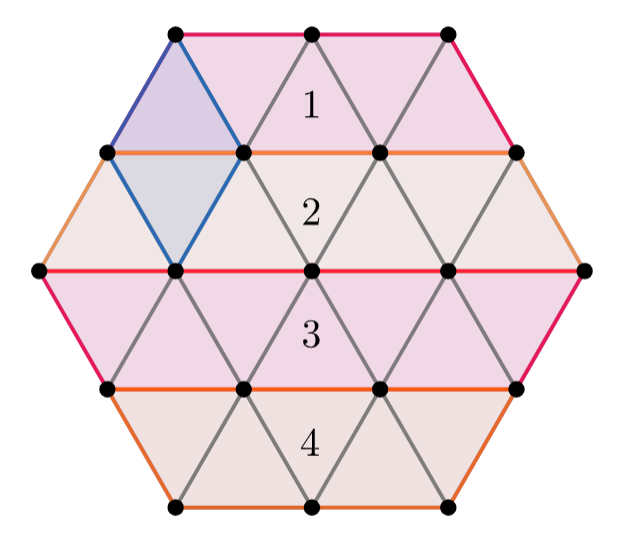
Estigui on estigui, ara la fila 2 està separada en dues parts, les dues amb nombre de caselles senar. Per tant en cadascuna hi ha al menys un diamant vertical. I de fet es pot veure, igual que abans, que cal exactament un diamant vertical. Finalment, en la fila 3 queda una part amb nombre de caselles senar (i possiblement algunes parts amb nombre de caselles parell, que requereix un quart diamant vertical. I si examinem en detall, es pot veure que cal exactament un diamant més. De manera que hem demostrat que cal al menys quatre, i com mostra la figura següent, amb 4 es pot. Així que la resposta és: $\boxed{4}$.
NOTA: Observem de fet que hem demostrat no només que cal al menys 4, sinò que cal exactament 4. I el mateix raonament que hem utilitzat el podríem generalitzar: si l'hexàgon fos de costat $n$ subdividit en equilàters de costat 1, el nombre de diamants verticals necessaris seria $n^2$, igual al nombre necessari d'horitzontals orientats a la dreta i els orientats a l'esquerra.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | SansUDR | SansUDR | 3 de maig de 2023 a les 14:13 | 03/05/2023 |
| Or | Nachulus | Nachulus | 3 de maig de 2023 a les 14:14 | 03/05/2023 |
| Or | oripq | oripq | 3 de maig de 2023 a les 14:15 | 03/05/2023 |
| Or | Hypergg2000 | Hypergg2000 | 12 de maig de 2023 a les 23:05 | 12/05/2023 |
| Or | Leyang.Xino | Leyang.Xino | 22 de maig de 2023 a les 13:11 | 22/05/2023 |
| Or | martinos | martinos | 31 de maig de 2023 a les 23:33 | 31/05/2023 |
| Plata | S05 | S05 | 19 de maig de 2023 a les 13:49 | 19/05/2023 |
| Xocolata | Pepyto_1932 | Pepyto_1932 | 18 de maig de 2023 a les 10:07 | 18/05/2023 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Oriol47 | Oriol47 | 1 de maig de 2023 a les 9:15 | 01/05/2023 |
| Or | mellamanhy | mellamanhy | 3 de maig de 2023 a les 14:13 | 03/05/2023 |
| Or | Alejandro | Alejandro | 7 de maig de 2023 a les 13:09 | 07/05/2023 |
| Or | Anton | Anton | 10 de maig de 2023 a les 7:13 | 10/05/2023 |
| Or | montserrat... | montserrat.muria | 11 de maig de 2023 a les 17:32 | 11/05/2023 |
| Or | arakelov | arakelov | 26 de maig de 2023 a les 14:06 | 26/05/2023 |
| Or | joseprivera | joseprivera | 31 de maig de 2023 a les 10:35 | 31/05/2023 |
| Or | jaquerol | jaquerol | 31 de maig de 2023 a les 21:28 | 31/05/2023 |
| Plata | PauC_SQV | PauC_SQV | 19 de maig de 2023 a les 13:50 | 19/05/2023 |
| Plata | Hiperboloide | Hiperboloide | 28 de maig de 2023 a les 17:31 | 28/05/2023 |
| Bronze | aram | aram | 20 de maig de 2023 a les 18:24 | 20/05/2023 |
| Xocolata | fakeone | fakeone | 12 de maig de 2023 a les 23:01 | 12/05/2023 |
