Comencem amb un triángle rectangle isòsceles que té vèrtexos $(0,0),(0,1),(1,0)$. A cada pas, separem el triangle en dues parts iguals traçant la bisectriu de l'angle de $90^\circ$; i ens quedem amb la meitat que està a la dreta des de la perspectiva de l'angle de $90^\circ$. Aquests serien els vèrtexos oposats a la hipotenusa dels primers $4$ triangles així generats. Els seus triangles han estat pintats de colors cada vegada més càlids.
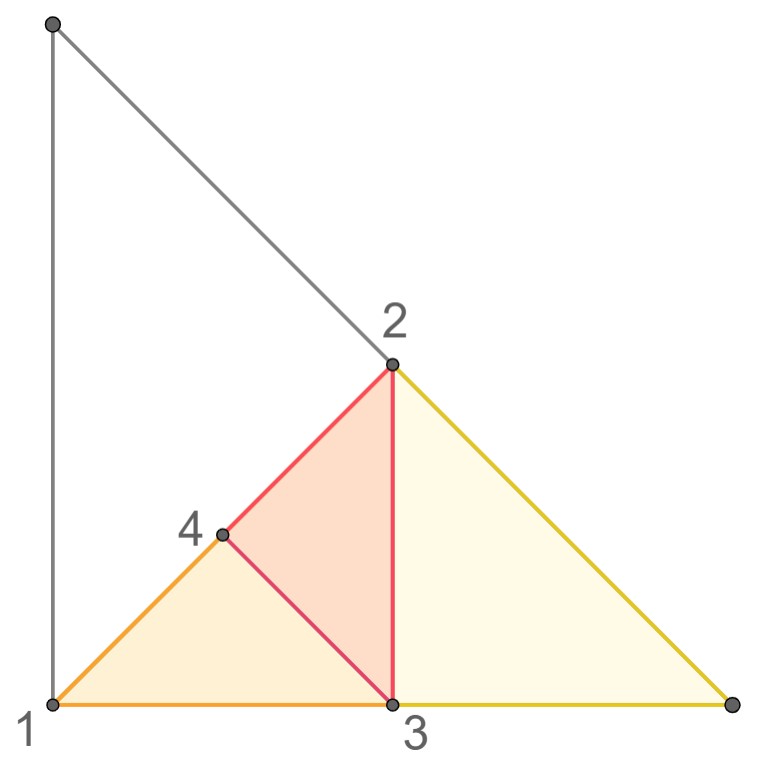
Amb aquest procediment, tindrem una successió de triangles rectangles, cada vegada més petits. Volem que trobeu les coordenades $(x,y)$ del punt al que convergeixen els vèrtexos de $90^\circ$ de cadascun dels triangles.
Com a resposta d'aquest problema, doneu el número $100x+10y$.
Considerem en cada passa quin canvi de posició està fent el vèrtex de l'angle de $90^\circ$. Si calculem la suma infinita de tots aquests vectors, trobarem el desplaçament final total del vèrtex i, per tant, la seva posició final. Ara, pots relacionar el vector en un pas amb el vector del següent pas?
Observant la geometria de la configuració, observem que l'angle entre dos vectors consecutius és sempre de $135^\circ$ en sentit horari, i que cada segment té longitud $1/\sqrt{2}$ per la longitud de l'anterior. Aplicant aquests fets podem trobar tots els vectors desplaçament. Els primers són: $$ (1/2,1/2), (0,-1/2), (-1/4,1/4), (1/4,0), (-1/8,-1/8), (0,1/8), (1/16,-1/16), (-1/16,0)...$$
Pots aprofitar els patrons per tal de cacular la suma infinita de tots aquests vectors?
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data |
|---|
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | montserrat... | montserrat.muria | 4 de març de 2023 a les 18:27 | 04/03/2023 |
| Or | JABorrás | JABorrás | 31 de març de 2023 a les 22:17 | 31/03/2023 |
| Plata | lorodane | lorodane | 1 de març de 2023 a les 4:55 | 01/03/2023 |
| Plata | arakelov | arakelov | 1 de març de 2023 a les 10:54 | 01/03/2023 |
