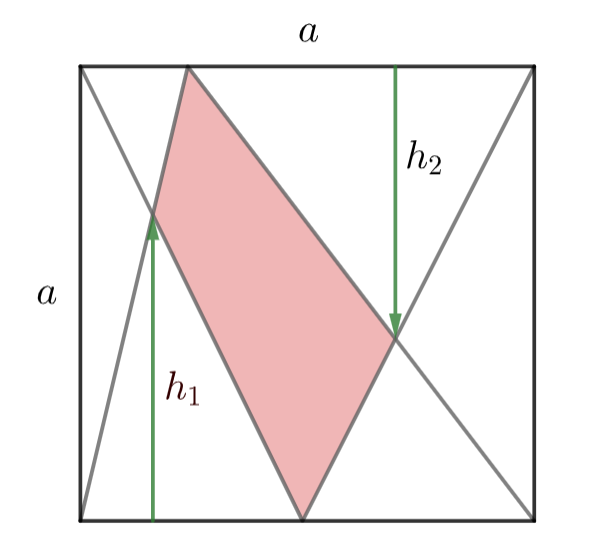
Si sabem que $a=10,h_1=7,h_2=8$ quant val l'àrea en vermell?
Per calcular l'àrea ens convé subdividir la regió vermella en polígons dels que sigui fàcil calcular l'àrea. Dibuixem paral·les a la base pels punts d'intersecció entre els costats dels triangles, com en la figura.
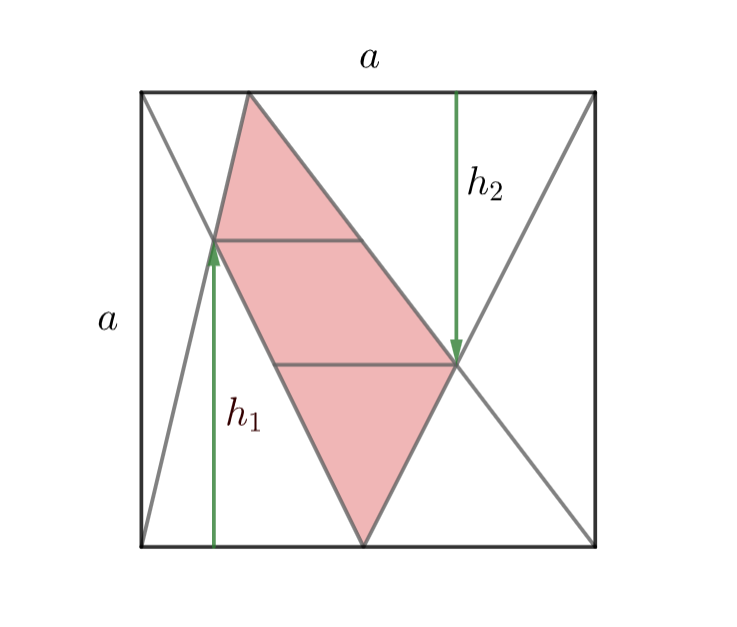
Ara l'únic que ens caldria seria averiguar els valors de les bases i les altures dels triangles vermells. Les altures són senzillament $a-h_1,a-h_2$ i el que és més complicat és calcular és les bases. Però el triangle vermell de dalt és semblant al triangle gran amb la base a sota. Com que aquest triangle té una base igual a l'altura, el triangle petit de dalt també. I concloem que la base del triangle vermell de dalt és $a-h_1$. De la mateixa manera, la base del triangle vermell de sota és $a-h_2$. Ja tenim totes les dades, ara falta calcular.
Calculem l'àrea del triangle de dalt $(a-h_1)^2/2$, l'àrea del triangle de sota $(a-h_2)^2/2$ i l'àrea del trapezi en mig $(h_1+h_2-a)(a-h_1+a-h_2)/2$. Aleshores si sumem i expandim trobem que l'àrea és: $$ [a^2-2ah_1+h_1^2 + a^2 -2ah_2 +h_2^2 + 2ah_1 -h_1^2 -h_1h_2 + 2ah_2 -h_2^2-h_1h_2 - 2a^2+ah_1+ah_2]/2 = \frac{1}{2}a(h_1+h_2) - h_1h_2$$
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data |
|---|
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Plata | trident23 | trident23 | 21 d’octubre de 2023 a les 14:10 | 21/10/2023 |
