En una graella rectangular $3\times 6$, escullim algunes de les caselles i les anomenem prohibides. Connectem les caselles restants en un camí que sempre va d'una casella a una veïna amb la que comparteix un dels costats. Si això es pot fer només d'una manera passant per totes les caselles no prohibides, diem que la configuració és "lineal". Quin és el mínim de caselles prohibides que cal escollir per tal que la configuració sigui "lineal"?
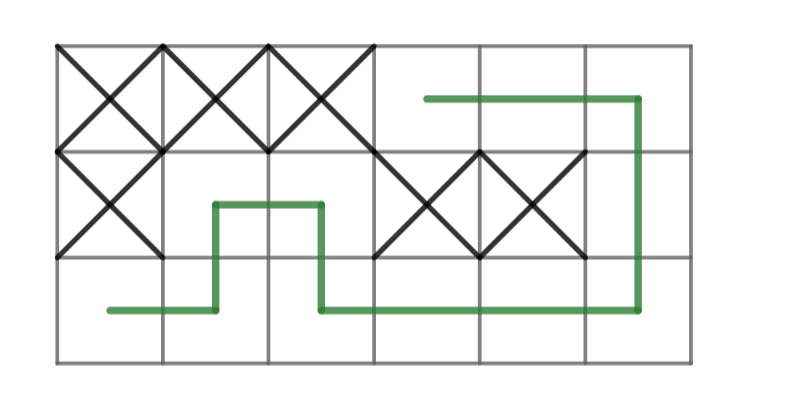
Per trobar el mínim, intentem fer una configuració lineal amb el mínim de caselles prohibides.
Per tal de fer una configuració que sigui lineal, és molt útil agafar configuracions on hi hagi una casella no prohibida que només està connectada a una altra casella no prohibida. Aleshores aquesta casella deu ser el començament o el final del camí. De fet, si prohibim una casella que estigui en el centre del costat esquerre, ja tenim definits un començament i un final.
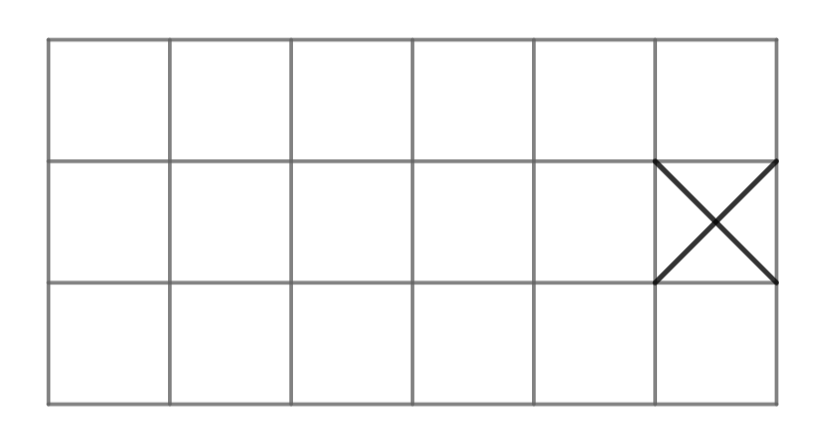
Però si només posem aquesta casella prohibida, encara hi ha diversos camins possibles que passen per totes les caselles possibles. Com podeu escollir caselles prohibides que forcin un únic camí?
La manera de fer-ho és afegir dues caselles més, i la primera és col·loca com en la figura:
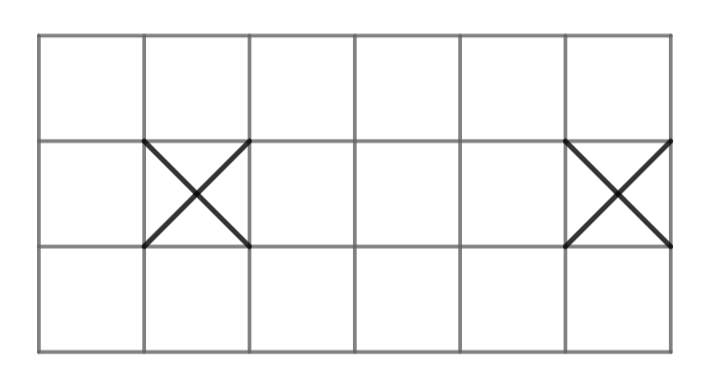
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data |
|---|
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data |
|---|
