Considerem un hexàgon regular d'àrea $1$. Diem que un punt de l'interior del pentàgon és central si sempre que tracem un segment des del punt fins a un vèrtex, els angles formats són aguts (la figura n'és un exemple). Siqui S el conjunt de punts centrals. Calcula l'àrea de S i introdueix la resposta arrodonida a dos decimals (i amb punt per separar decimals; per exemple 1.72).
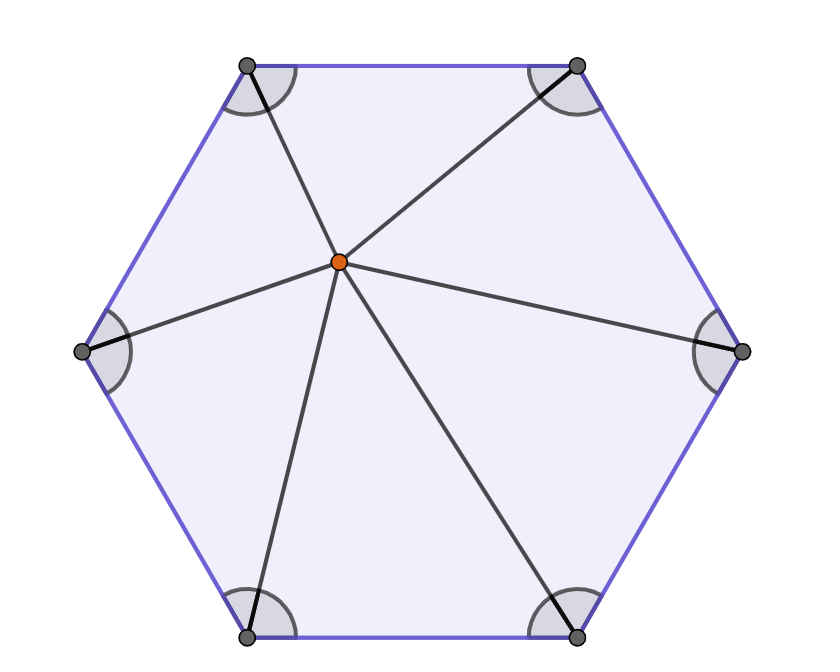
Si tracem tots els segments des d'un punt P fins als vèrtexos, es formen $6$ triangles. Ens fixem en un costat de l'hexàgon, el seu triangle associat i els dos angles de la base.
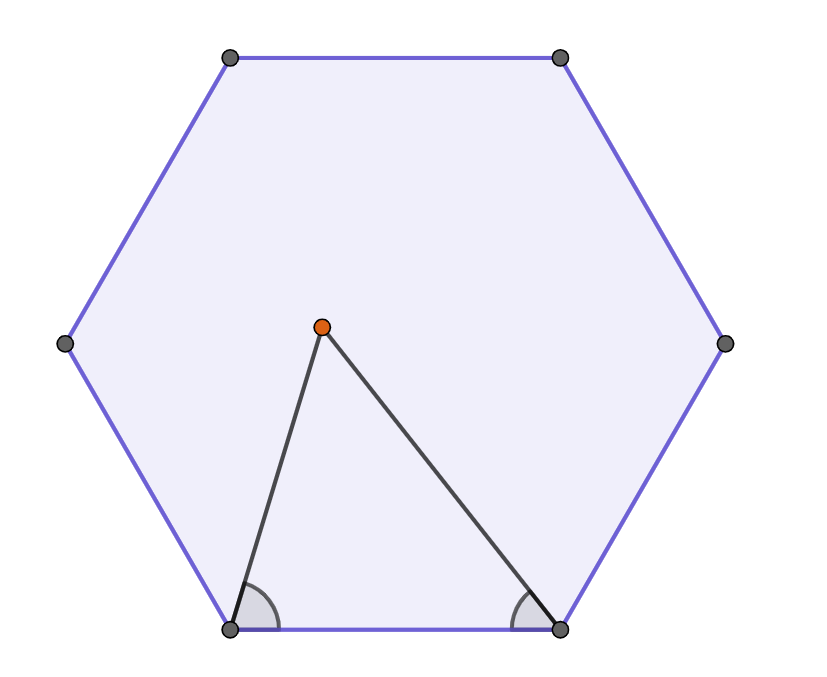
Per tal que aquests dos siguin menors que $90$º, cal que el punt P estigui entre les perpendiculars al costat que passen pels extrems del costat.
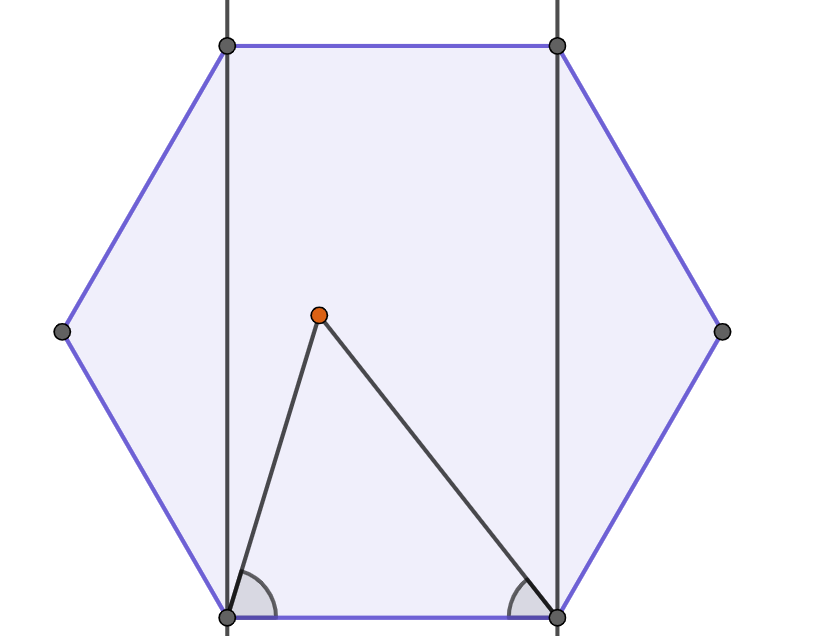
La intersecció d'aquestes regions per cada costat és el conjunt S del que volem trobar l'àrea.
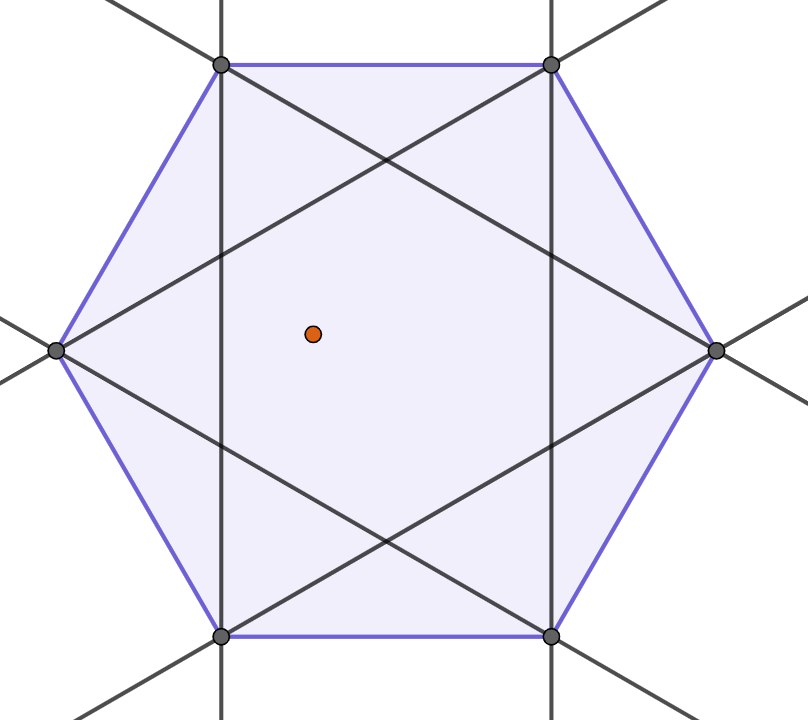
Ara queda que trobis l'àrea d'aquesta regió S, que resulta ser un hexàgon. Intenta trobar el costat o el radi i calcula-hi l'àrea.
Es pot relacionar l'apotema de l'hexàgon original amb el radi del hexàgon S. Considerem el centre $C$ de l'hexàgon. Considerem un costat, els seus extrems $A$,$B$, el punt mig $J$ i el punt $I$, un vèrtex de l'hexàgon S, tots com en la figura.
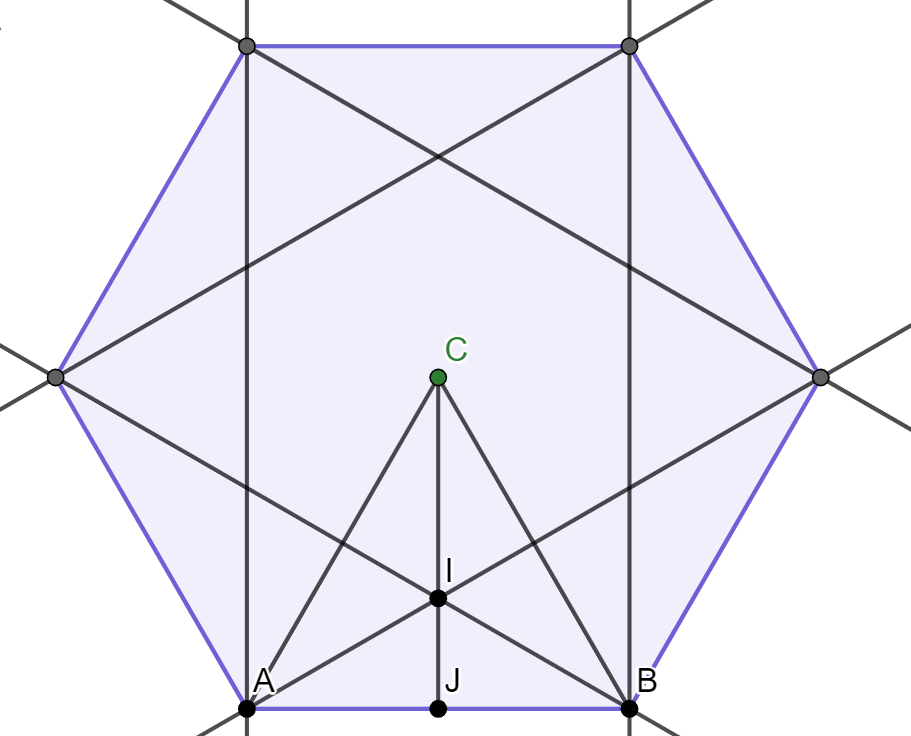
Llavors, siqui $l$ la llargada del costat de l'hexàgon original. $ABC$ és un triangle equilàter, així que fent una mica de trigonometria treiem que la seva altura és $l\sqrt{3}/2$. Per calcular $IJ$ ens fixem en que $AIJ$ és un triangle rectangle d'angles $30,60,90$º. Per tant, com que $AJ= l/2$, multiplicant per la tangent de $30$º, tenim que $IJ=l/2\sqrt{3}$. Per tant, $CI=CJ-IJ=l\sqrt{3}/3$.
Si el radi és aquest, quina és l'àrea de l'hexàgon S? Recorda que l'àrea de l'hexàgon original era $1$.
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Plata | PolGomez | PolGomez | 2 de febrer de 2024 a les 12:38 | 02/02/2024 |
| Xocolata | tristany | tristany | 21 de febrer de 2024 a les 8:39 | 21/02/2024 |
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | arakelov | arakelov | 1 de febrer de 2024 a les 6:34 | 01/02/2024 |
| Or | carlagual | carlagual | 2 de febrer de 2024 a les 12:32 | 02/02/2024 |
| Or | iannualart | iannualart | 2 de febrer de 2024 a les 12:33 | 02/02/2024 |
| Or | Superep | Superep | 28 de febrer de 2024 a les 9:07 | 28/02/2024 |
