Els sòlids platònics són objectes molt bonics, que tenen totes les cares com polígons regulars tots iguals. Els sòlids arquimidians són menys coneguts però també molt bonics. Totes les seves cares són polígons regulars (potser no totes són el mateix polígon) i tots els vèrtexos són equivalents.
Un exemple és el cub truncat, que es pot aconseguir retallant les cantonades d'un cub. Tenim un cub de costat $4$ i volem truncar-lo. Per fer-ho cal escollir una distància $x$. Al voltant de cada cantonada marquem els punts de cada aresta que estan a distància $x$ de la cantonada. Llavors fem un tall que passa pels tres punts que hem marcat. Quin deu ser el valor de $x$ per tal que totes les cares siguin regulars? (dona la resposta amb dos decimals i usa un punt per separar la part entera de la decimal.)
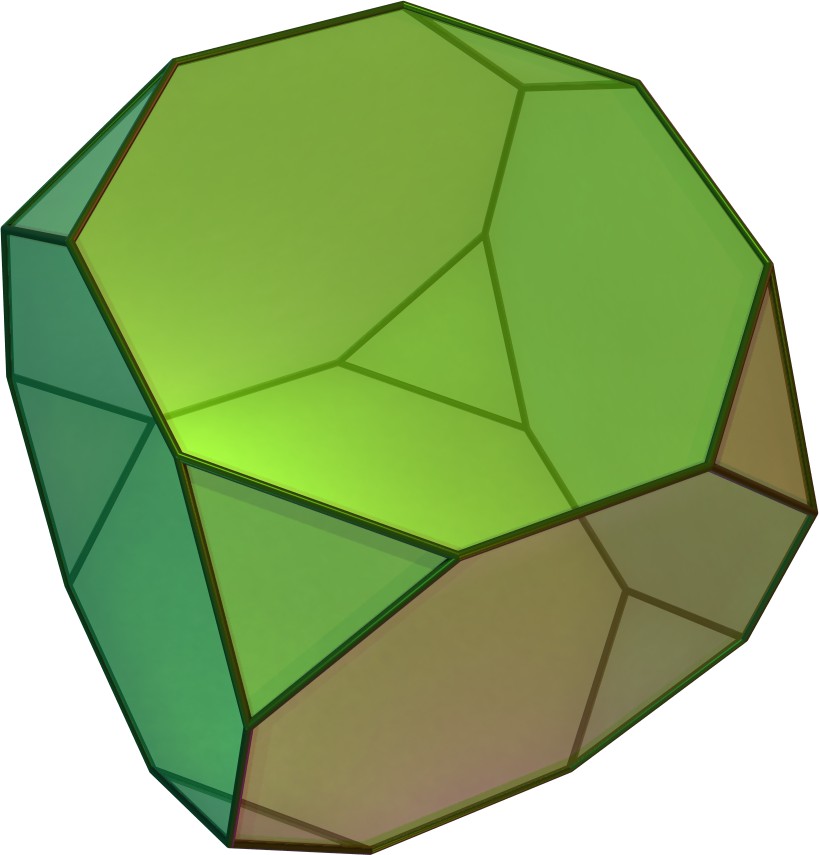
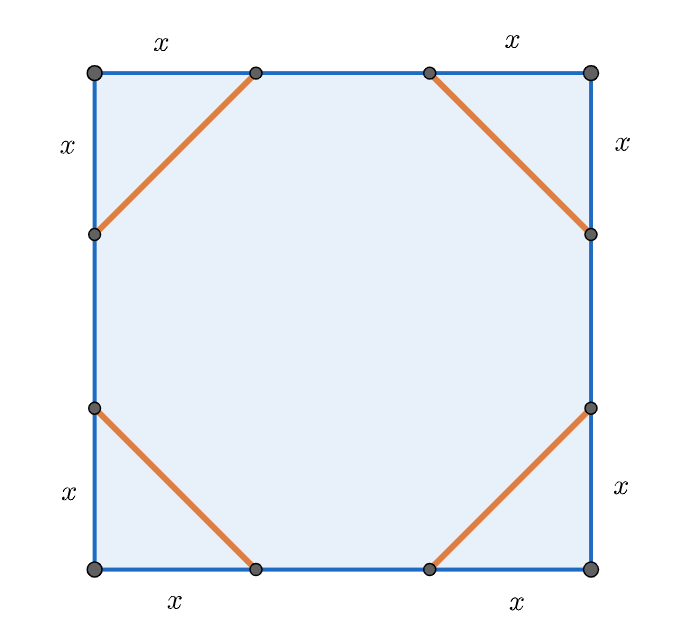
NOTA: La imatge de la dreta ilustra els talls del cub des de la perspectiva d'una de les cares. La imatge de l'esquerra és una representació del cub truncat en 3D ( "A truncated regular hexahedron" by Cyp -- CC BY-SA 3.0 DEED)
La condició que cal que es compleixi és que tots els costats del nou octògon mesurin el mateix, tant els verticals i horitzontals com els diagonals. Com que el costat mesurava $4$ el nou costat vertical o horitzontal mesura $4-2x$, mentre que el diagonal podem calcular per Pitàgores que mesura $x\sqrt{2}$.
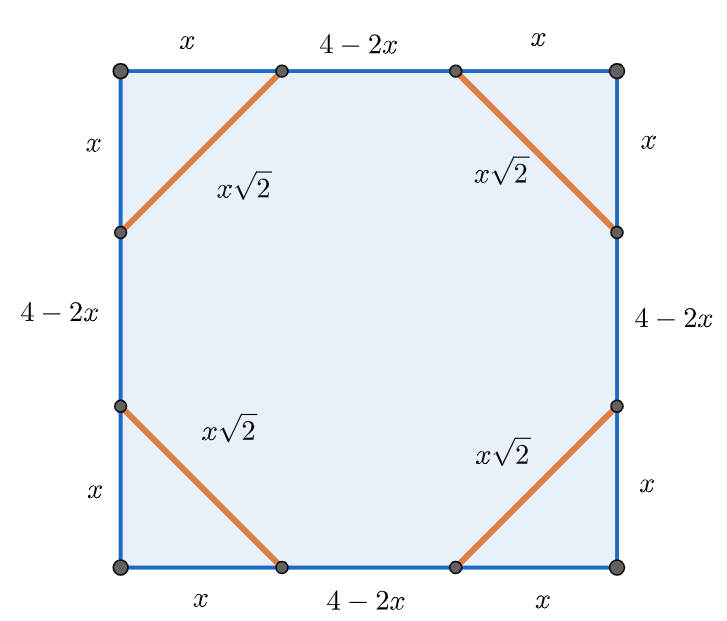
Cal resoldre l'equació $4-2x = \sqrt{2} x$, que és equivalent a que $x = 4/(2+\sqrt{2})$. Multiplica per sobre i per sota pel conjugat per trobar el valor de $x$.
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | carlos_paz | carlos_paz | 22 de gener de 2024 a les 10:27 | 22/01/2024 |
| Xocolata | sapoce | sapoce | 22 de gener de 2024 a les 13:12 | 22/01/2024 |
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Albi | Albi | 10 de gener de 2024 a les 14:04 | 10/01/2024 |
| Or | arakelov | arakelov | 27 de gener de 2024 a les 20:30 | 27/01/2024 |
| Plata | Superep | Superep | 3 de gener de 2024 a les 14:58 | 03/01/2024 |
| Plata | RamonCanet | RamonCanet | 16 de gener de 2024 a les 9:51 | 16/01/2024 |
| Bronze | zmp | zmp | 6 de gener de 2024 a les 20:31 | 06/01/2024 |
