Considerem un quadrat de costat $1$. Anomenem "regió propera" del quadrat a la regió formada pels punts del pla des dels quals es veu el quadrat amb un angle major o igual a $90^\circ$.
Definim l'angle amb que es veu una figura des d'un punt $P$ com l'angle més petit centrat en $P$ que inclou la figura. O sigui, l'angle entre el punt més a l'"esquerra" i més a la "dreta", mirant des de $P$. La següent figura n'és un exemple pel punt blau.
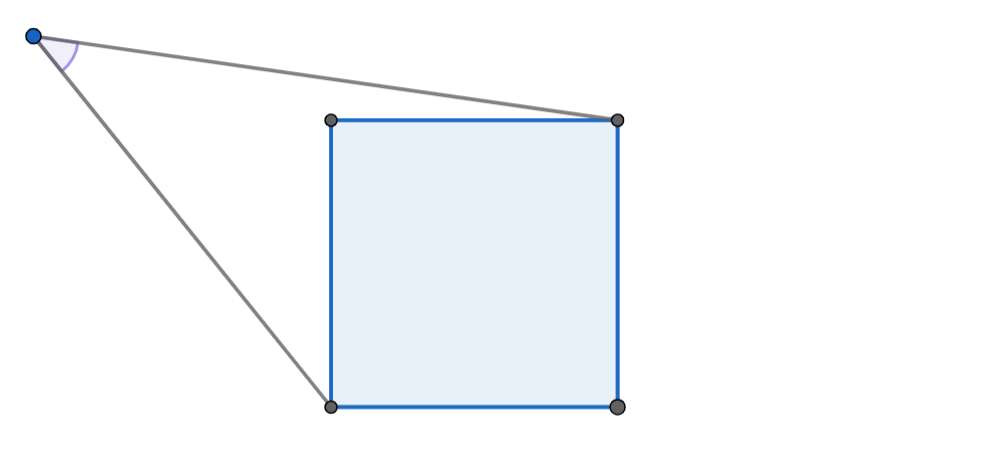
Quina és l'àrea de la regió propera al quadrat? (responeu amb dos decimals i useu el punt per separar unitats de decimals).
Si ens apropem dins del pla, l'angle amb que veiem el quadrat augmenta, per tant podem considerar la vora de la regió propera (que serà la regió on es vegi amb angle d'exactament $90^\circ$). Llavors la vora separarà el pla en dues regions, i volem l'àrea de la "interior", on es veu amb angle major o igual a $90^\circ$.
Veure el quadrat vol dir veure algun dels seus costats. Pots trobar la corba de punts amb que es veu un dels costats amb angle $90^\circ$? Potser et sona, es diu arc capaç.
Un costat és un segment de llargada $1$, i donat un segment, la corba de punts des d'on es veu un segment amb angle fix és un arc capaç, que en el cas particular de l'angle de $90\circ$, és un semicercle que té el segment per diàmetre. Llavors, la regió des d'on es veu un costat amb angle major o igual a $90\circ$ és un semicercle de radi $1/2$.
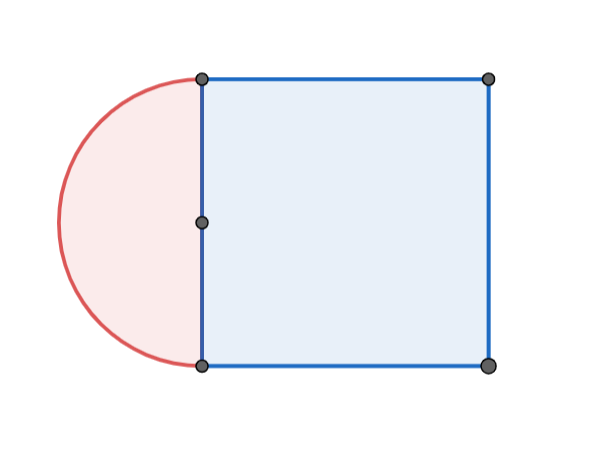
També podria ser que es vegin dos costats a la vegada i tots dos junts es vegin amb un angle de $90^\circ$. Però si això passa, llavors, estem veient una diagonal del quadrat amb angle de $90^\circ$. Això de nou, només passa en un arc capaç. Quan el tracem, veiem que tota la regió des de la que es veuen dos costats queda fora.
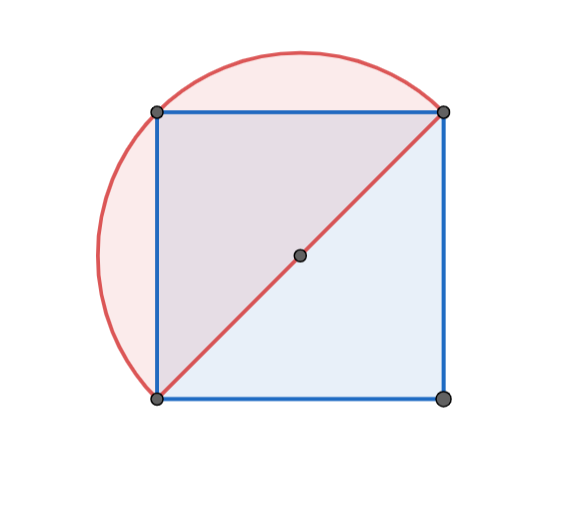
Per tant, des d'on es veuen dos costats sempre es veuen amb un angle menor o igual a $90^\circ$.
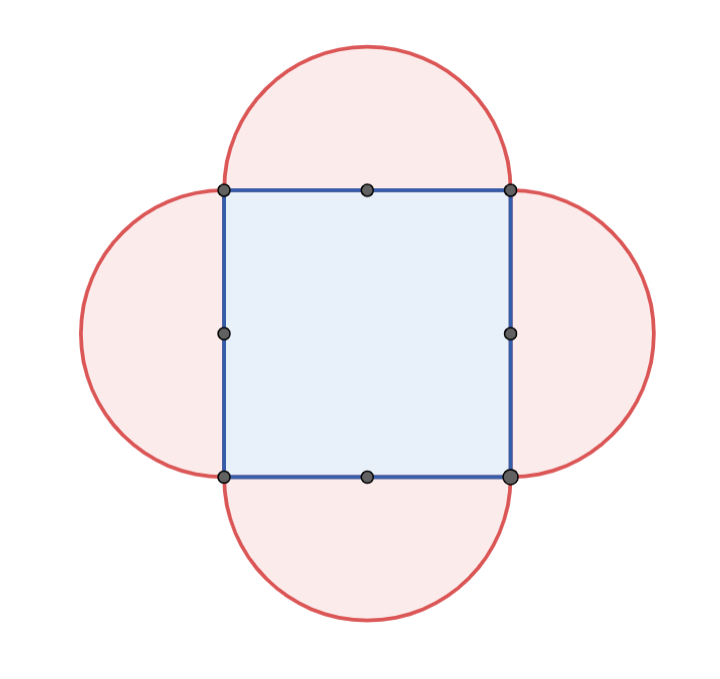
Llavors, pots calcular l'àrea dels quatre semicercles?
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | TomeuAndreu | TomeuAndreu | 15 de setembre de 2024 a les 18:41 | 15/09/2024 |
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | arakelov | arakelov | 27 de setembre de 2024 a les 21:06 | 27/09/2024 |
| Bronze | Pep123 | Pep123 | 15 de setembre de 2024 a les 17:11 | 15/09/2024 |
